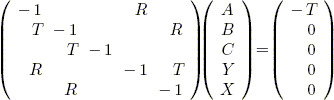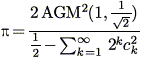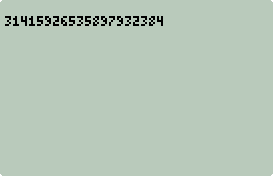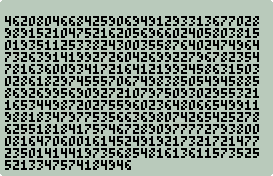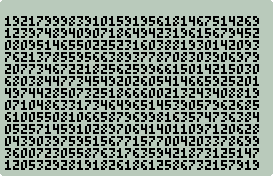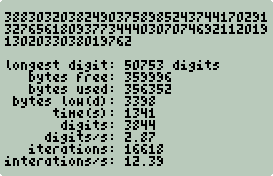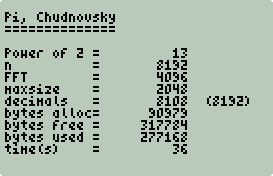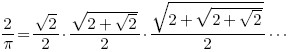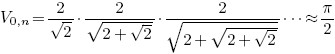Extend your 50g with C
Document Version: 1.12 (Dec 09 2008) (See Change
Log).
HPGCC Version: 2.0SP2
Author: Egan Ford (egan NO_SPAM_AT sense.net).
Contents
Extend your 50g with C - Part 1
Introduction
Why C?
Why not C?
HPGCC
Disclaimer
Development Environment
Hardware Requirements
Software Requirements
User Requirements
Cygwin/X Installation (Windows Only)
HPGCC w/ Extras Installation
Windows
Linux
OS/X
HPGCC 2GB SD Card Support
Sidebar: Play First!
ARM Toolbox Installation
Setup Environmental Variables
Getting Started with HPGCC
Hello, World
Crashes
Hangs
Wrappers
Data Types
C Binaries Are Big, Too Big
Base Template
Extend your 50g with C
Debugging
HPAPINE 101
Makefiles
Support
Summary
Extend your 50g with C - Part 2
How to Follow the Examples
The Examples
Example: Real and Complex LogGamma
Building c9x-complex
Get a Complete libm.a
LogGamma
Makefile
Wrapper
LogGamma
Test
Summary
Example: Sparse Linear Solver
CSparse Library
CSparse Front-end
Makefile
Wrappers
N Panes Problem
N Panes Application
Dense vs. Sparse
HPStack and HPParser
Installing HPStack/HPParser
csparse2.hp
Wrappers
HPStack Issues
Summary
Example: π Shootout
Measuring Performance
Checking Accuracy
Check
π Wrapper
π Shootout Makefile
Chudnovsky
String to File
String to File Wrapper
Chudnovsky Wrapper
Run It/Check It
Gauss AGM
AGM Wrapper
Run It/Check It
Spigot Algorithm
Spigot Wapper
Run It/Check It
Unbounded Spigot Algorithm
LibTomMath
Unbounded Spigot π
uspi Wrapper
Run It/Checkit
Breaking the 32373 Barrier
Sidebar: Next Prime
Next Prime Wrapper
Next Prime Shootout
Machin
Machin Wrapper
Run It/Check It
More
Arctangents: Euler, Gauss, Takano, Størmer, et al
piatan Wrapper
Run It/Check it
Current Standings
Chudnovsky Revisited
sspi Wrapper
sspi Run It/Check It
And the Winner is...
ARM/C vs.
Saturn/Assembly, Machin vs. Machin, Mano-a-Mano
Summary
Example: Computational Geometry Library
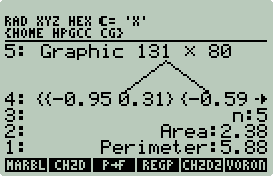
2D Convex Hull
Marbles
Marbles Wrapper
Convex Hull 2D
Convex Hull 2D Wrapper
Sidebar: P2F
P2F Makefile
P2F Wrapper
Convex Hull 2D II
Convex Hull 2D II Makefile
Convex Hull 2D II Wrapper
Sidebar: Screen Capture
Voronoi
Diagrams
Voronoi Makefile
Voronoi Wrapper
Random Square/Circle
Computational Graphics Library
Extend your 50g with C -
Part 3 - More Examples
How to Follow the Examples
The Examples
Viète Accelerated
Introduction
Implementation Constraints
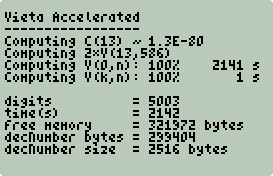
Results
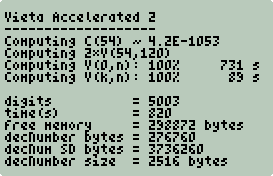
Trial 1
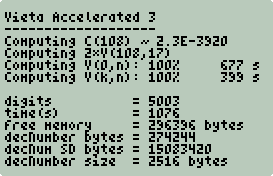
Trial 2
Trial 3
Finding the optimal k and
n
Viète
vs. The World
The Code
Wrapper
Usage
Code with Comments
libfsystem
for Arrays
Arbitrary Text Cursor Positioning
Computer Generated UserRPL Code
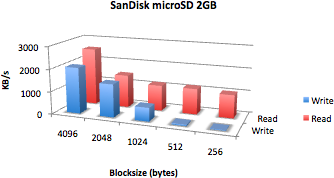
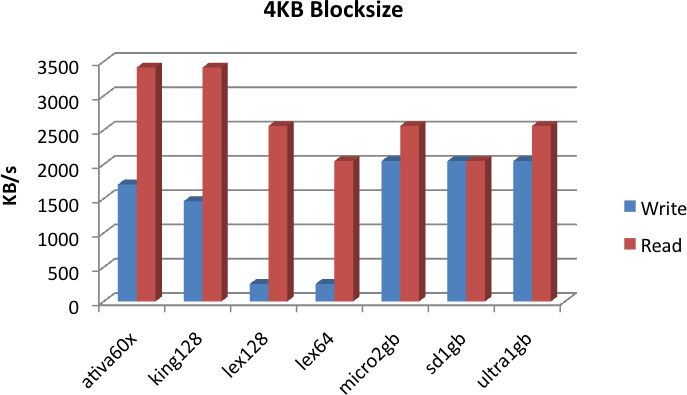
Sidebar: Memory Card Performance
Final Words
UPDATE: Iterative vs.
Recursive
Summary
Thanks
References
Change Log
Extend your 50g with C - Part 1
Introduction
This lengthy article explains why you would
and how you can extend the functionality of your 50g using C. Complete examples are provided to illustrate how to create high performance
mathematical routines such as a complex LogGamma function, a sparse linear
solver, and a 2D convex hull.
There are two reoccurring themes in this article:
-
Keep it simple and use the right tool for the right job.
C is not a complete replacement for UserRPL. E.g. C it can require a lot of
code to do what UserRPL does in one or two commands when processing stack
arguments. One the other hand C is faster than Saturn assembly for
intensive computation. C is also a lot easier to read, write, and debug
with larger applications.
-
Do not reinvent the wheel.
There is a lot of freely
available mathematical C code available. Most of the examples will focus
on using freely available C code.
This article is not a replacement for HPGCC, C, or 50g
documentation. This article is structured more like a tutorial.
In-depth knowledge of C is not required. It is possible for a person
without any C experience to compile and run all the examples. However, you
will get more out of this article if you know C. If you want to learn C
then I suggest one or both of the follow texts:
-
The C Programming Language, 2nd ed., by Kernighan
and Ritchie. This is the C book, and is frequently referred to as
K&R. This book is short and sweet (about 1cm thick). If you grasp
the obvious then this is the book for you. I learned C from the first
edition. The first edition is a collectors item now, I wish I had kept mine
when I got the 2nd edition.
-
C Primer Plus, 5th ed., by Stephen Prata.
Chatty and verbose, many find this bible sized text easier to understand than
K&R. More demanding topics like pointers and structures are well
documented in this text.
Why C?
-
C is fast, very fast.
-
There is an abundance of freely available quality mathematical C
code and libraries. This will save you a lot of time.
-
Rapid development and prototyping. Every example here
was written for my workstation first, then ported to the 50g in seconds.
-
Skill reuse. C skills (unlike SysRPL and Saturn
Assembly) have use almost anywhere. 50g C programming is an example of
embedded programming. Embedded cross-compiling, object size optimization,
and debugging skills have many applications elsewhere.
-
Portability. With little effort you can rebuild your
50g C applications for PCs, Macs, PDAs, and even TI calculators (TIGCC).
-
C is cool.
Why not C?
HPGCC
HPGCC is a cross-compiler suite available for x86 Linux,
Mac, and Windows capable of creating 50g ARM binaries. With some effort
HPGCC can be compiled for almost any platform. HPGCC is based on GCC (GNU
Compiler Collection). The GNU Compiler Collection includes front ends
for C, C++, Objective-C, Fortran, Java, and Ada, as well as libraries for these
languages (libstdc++, libgcj,...) [1].
Officially HPGCC 2.0SP2 only
supports C, however Jean-Yves Avenard created Mac and Linux versions that also
support C++ [2]. With little effort other languages like Fortran could
also be added. Imagine compiling your existing Fortran code for your 50g.
It would probably run faster than the computer it was originally coded for!
Unlike UserRPL, SysRPL, and Saturn Assembly, 50g ARM binaries run outside of the 50g UserRPL
environment. This has a few advantages, e.g. speed and access to more
memory. HPGCC creates a
contiguous memory block of the unused port 0 and 1 memory as usable application
memory, plus there is a bonus 90KB of RAM unused by the 50g OS. That's a
total of 459KB (assuming the Ports 0 and 1 are empty). Although 50g ARM
binaries run outside of UserRPL it is still possible to interact with the stack.
Disclaimer
Use at your own risk. Although nobody has reported
bricking their 50g with HPGCC, I suppose anything is possible. I imagine
that the worse that could happen is that you break the reset button because of
the countless times you had to reset it. I've only had one scare. A
crash put lines in the overscan area of the LCD that persisted after a hard
reset, after 10 or so seconds it faded away. I wasn't too scared, because
I did it over and over again to see what would happen.
I'm not an expert at C, the 50g, or HPGCC. I have tried to be as
accurate and thorough as possible. Omissions and mistakes are most likely
present. Again, use at your own risk.
Enjoy.
Development Environment
Hardware Requirements
-
A 50g. Believe it or not you can do a lot of
development and testing without one, but eventually you are going to have to
test it on the real thing. NOTE: EMU48 with 50g emulation
only emulates the Saturn processor emulation of the 50g, i.e. EMU48 cannot
execute ARM binaries.
-
A 50g USB or Serial cable. I find the 50g USB cable
to be the better solution since it also provides power to the 50g. Some
have had problems with USB file transfers and opt for the serial cable.
The best serial cable for the 50g can be obtained here:
http://commerce.hpcalc.org/serialcable.php.
-
An SD Card reader. I prefer the SanDisk MicroMate
because I can easily remove the SD Card from the reader without having to snap
it in to some type of shell. Any will do, I just happen to have this
laying around. This one looks good:
http://commerce.hpcalc.org/cardreader.php.
-
An SD Card. Any size will do with 10MB free space.
I am using an old 128MB Lexar SD Card. 128MBs is like infinity.
-
A paper clip. You will never want to run a C program
on your 50g without one handy. In a pinch you can just remove a single AAA
battery for 1 second to get the same effect.
-
A workstation. Currently it is not possible to
compile C code on the 50g. It must be cross compiled with HPGCC.
Software Requirements
-
A workstation OS. This article was written for and
tested with Windows (XP and Vista), Linux, and Intel OS/X 5.5 (Leopard) but should be easy to adapt
to any UNIX.
-
Cygwin/X (Windows users only). This is not an HPGCC
requirement, just a requirement for this article. I find developing with
GNU tools easier with a Linux/UNIX shell. This also makes this article a
bit more universal. Cygwin/X is also
required when testing code on the PC. NOTE: All the HPGCC
source code will compile and link just fine using the native HPGCC Windows
tools.
-
The hpgcc.tgz
(Windows), the hpgcc-linux.tgz (Linux),
or the hpgcc-osx.tgz (OS/X) tarball. This tarball contains:
-
HPGCC 2.0SP2: The 50g C cross compiler for Windows, Linux,
or OS/X.
-
HPAPINE: A 50g simulator for testing 50g C code.
This is not an emulator. More on this later.
-
All the example code, makefiles, and binaries from this
article.
-
This document.
User Requirements
You should know how to:
Cygwin/X Installation
(Windows Only)
Skip if Linux or OS/X.
Cygwin/X is a GNU/Linux like environment for Windows.
It does not install any services or drivers, it is self-contained user space
software just like any other application. IOW, it is safe. (Standard
disclaimer applies.)
Cygwin/X adds the X Windows System to your Windows desktop.
X Windows is 10 (make that 11) times better than just MS Windows. For more
information about X Windows read:
http://en.wikipedia.org/wiki/X_Window_System. BTW, both Linux and OS/X
use X.
NOTE: Vista users note the exceptions.
-
Download
http://cygwin.com/setup.exe, virus scan it, execute it, install all
packages,
then take a nap. Cygwin/X download and install takes hours. Example
session:
Run setup.exe:
Click Next.
Click Next.
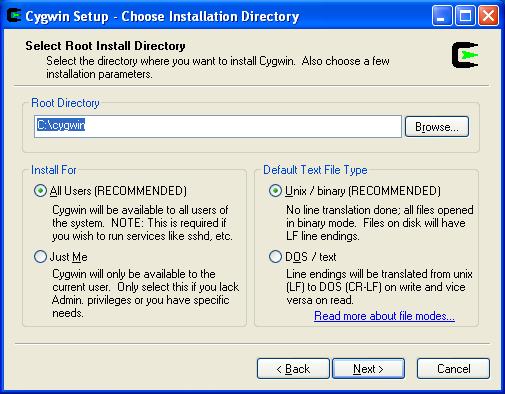
Click Next.
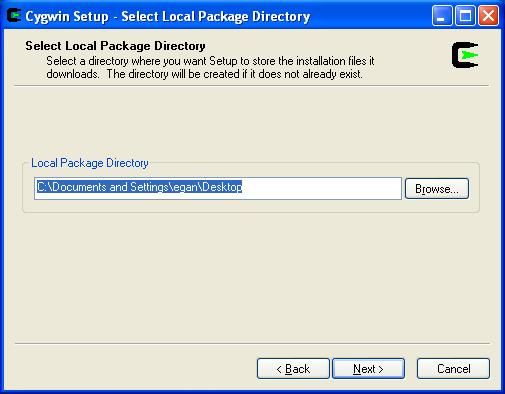
VISTA EXCEPTION: Change the default of c:\windows\system32 to c:\cygwin_install_files.
XP users can take the default.
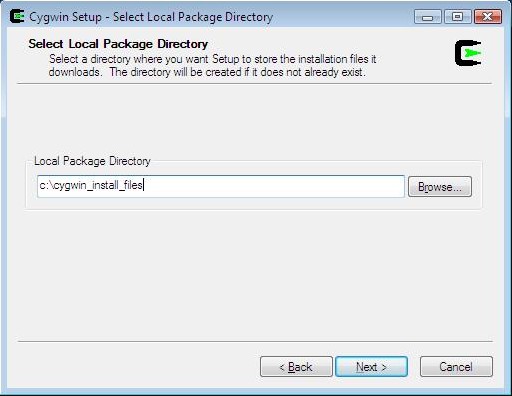
Click Next.
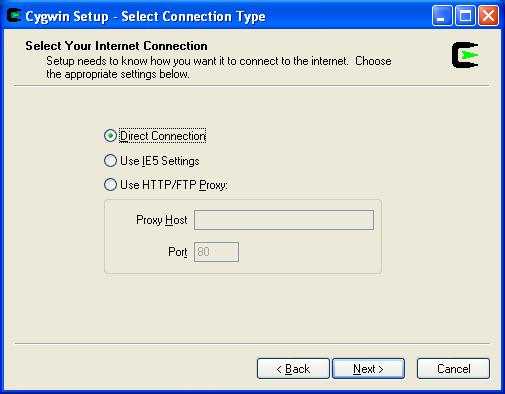
Click Next.
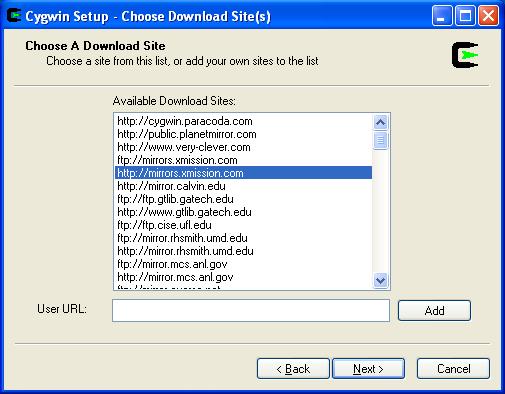
Select any mirror then click Next.
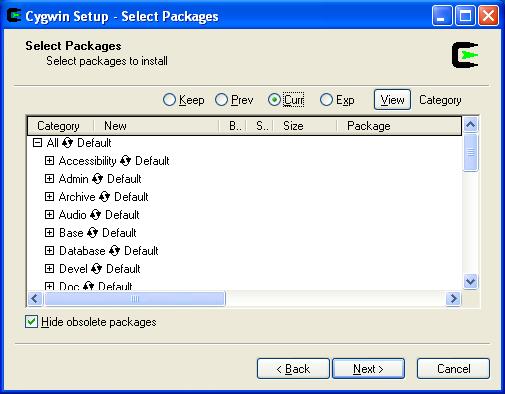
Click on the symbol between "All" and "Default" to change "Default" to
"Install".
NOTE: You can reduce disk space by just installing Devel and
X11.
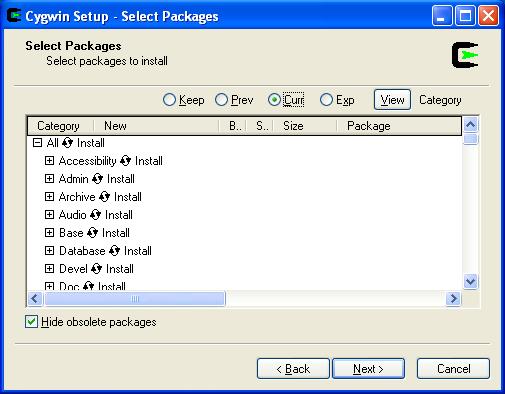
Before clicking Next, verify that your dialog matches the snapshot above.
I.e. All packages to be installed. Ok, click Next.
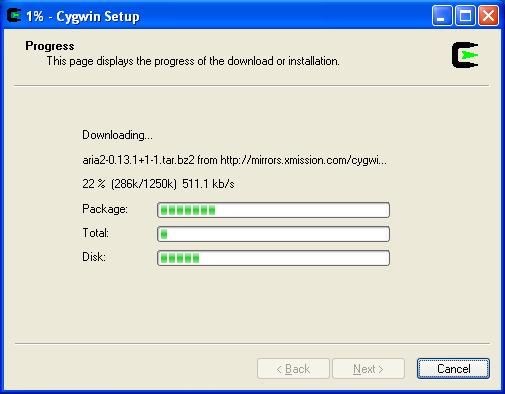
Take a nap, this could take hours.
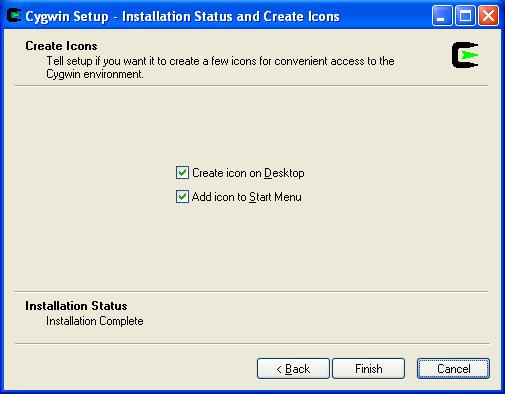
Click Finish. Congratulations you now have a GNU/Linux/UNIX like
development environment for Windows.
VISTA EXCEPTION: Vista users will get the following dialog:
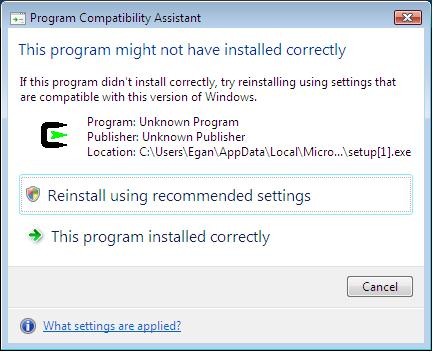
Select: "This program installed correctly".
-
Setup two icons anywhere you like.
-
StartX: C:\cygwin\usr\X11R6\bin\startxwin.bat
-
Xterm: C:\cygwin\bin\run.exe -p /usr/X11R6/bin xterm
-display 127.0.0.1:0.0 -ls
VISTA EXCEPTION (NOTE: works with XP too):
-
StartX: Just use the Start X-Server icon on
the desktop.
-
Xterm: Use Start Menu/All
Programs/Cygwin-X/xterm
-
Test. First run StartX. This only needs
to be run once. You'll notice an X in your tray. Right-click, exit
if you need to exit X. StartX also starts up an Xterm.
If you want multiple Xterms, then run Xterm. If all went
well you should see something like this:
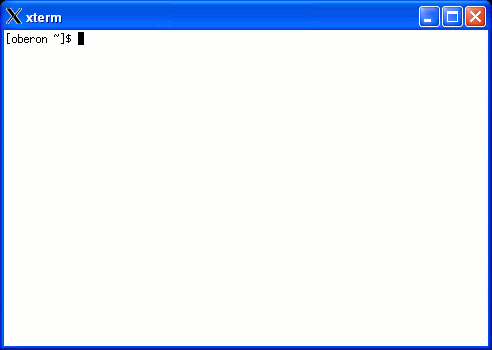
Congratulations you have a very powerful GNU/Linux
environment at your finger tips. NOTE: Cygwin/X paths are a
different than Windows paths. First, Cygwin/X uses the forward slash (/) as
the directory separator, and 2nd, C: is
replaced with /cygdrive/c. E.g.
my Windows home directory is C:\home\egan,
but from a Cygwin/X perspective it is /cygdrive/c/home/egan.
BTW, the ~ (tilde) is often used as a
short cut for the home directory, and will be used frequently in this article.
HPGCC w/ Extras Installation
Follow the instructions below for your platform.
After the platform specific install everything you will need will be self-contained in the
~/hpgcc directory.
Windows
Prerequisites: Cygwin/X install (above).
Open up an Xterm and type:
cd ~
(puts you in the root of your home directory)
wget
http://sense.net/~egan/hpgcc/hpgcc.tgz
tar zxvf hpgcc.tgz
Linux
Prerequisites: Development tools must be
installed (e.g. gcc, X11, and GTK).
From a command prompt type:
cd ~
(puts you in the root of your home directory)
wget
http://sense.net/~egan/hpgcc/hpgcc-linux.tgz
tar zxvf hpgcc-linux.tgz
OS/X
Prerequisites: X11 and Xcode (with X11
development support) must be installed. Tip: Install X11 first, then
Xcode. Both X11 and Xcode can be found on your installation media.
Launch X11 or startup a new xterm and type:
cd ~
(puts you in the root of your home directory)
wget
http://sense.net/~egan/hpgcc/hpgcc-osx.tgz
tar zxvf hpgcc-osx.tgz
HPGCC 2GB SD Card
Support
Part 3 of this document requires
libfsystem. After the initial
release of this document a bug was identified and fixed with
libfsystem that only affected 2GB SD
cards. To apply this patch open up an Xterm and type:
cd ~/hpgcc
wget
http://sense.net/~egan/hpgcc/2GB-libfsystem.tgz
tar zxvf 2GB-libfsystem.tgz
ARM Toolbox Installation
To run ARM binaries on the 50g you must have the ARM
Toolbox installed OR have had the binary converted to a standalone
executable using the ARM Toolbox. As a developer you will need the ARM
Toolbox, but if you convert the binaries to a standalone executable then you can
distribute your binaries without requiring that the ARM Toolbox be installed.
-
Copy the file ~/hpgcc/2.0SP2/sources/ARMToolbox/SETUP.BIN
to your 50g.
TIP: Windows users type in your Xterm window:
cd ~/hpgcc/2.0SP2/sources/ARMToolbox/
explorer .
This will open an explorer window in the ARMToolbox directory so that you can
drag and drop SETUP.BIN to the
Connectivity Kit.
-
On the 50g put the number 2 on the stack:
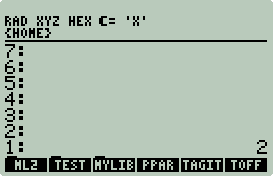
Next, put SETUP.BIN on the stack, not
'SETUP.BIN'. Your 50g should look
like this:
Now press
 ,
then
,
then  +
+ .
.
-
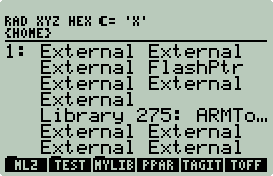
Verify that the ARM Toolbox is installed by pressing:
 .
.
Setup Environmental Variables
Each time you open a new Xterm type:
cd ~/hpgcc
. hpgccenv
(yes, that is .
SPACE hpgccenv)
This will setup your HPGCC and PATH environment for that
Window only.
Let the fun begin!
Getting Started with HPGCC
All the C source for this section is in
~/hpgcc/test.
Your 50g working directory should be home/hpgcc/test.
Hello, World
Lets start with the classic
hello, world from K&R:
#include <hpgcc49.h>
int main(void)
{
clear_screen();
printf("hello, world\n");
WAIT_CANCEL;
return(0);
}
There are a few differences from the classic
hello, world:
-
The header file hpgcc49.h
replaces the ubiquitous stdio.h.
hpgcc49.h is a collection of other
header files specific to HPGCC. Just about every HPGCC specific call is
defined in the hpgcc49.h collection.
-
clear_screen(),
while not entirely necessary, is generally a good idea if you plan to output text
directly to the screen. E.g. hello,
world with and without clear_screen():


-
WAIT_CANCEL, is
not necessary either, but, if you want to see your output before returning to
the 50g UserRPL environment you will need something that pauses for input.
WAIT_CANCEL waits for
the
 key to be pressed.
key to be pressed.
To build and run this example, type the following commands:
cd ~/hpgcc/test
make clean
make hello.hp
Next create a 50g home/hpgcc/test
directory and transfer hello.hp to that directory.
To run, press
 (you should see a lot of garbage), then
(you should see a lot of garbage), then

 .
To exit press
.
To exit press
 .
.
It is possible to make this a standalone executable that
does not require the installation of the ARM Toolbox. Press
 , then
, then

 . Then press
. Then press

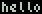 .
This will overwrite the
.
This will overwrite the
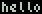 that required
that required
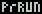 with a
with a
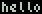 that can run without it. To run just press
that can run without it. To run just press
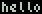 . Easy!
From this point forward all examples will be assumed to be standalone
executables.
. Easy!
From this point forward all examples will be assumed to be standalone
executables.
Hi Bob!
Next lets try something a bit more interesting:
1 #include <hpgcc49.h>
2 int main(void)
3 {
4 char *name;
5 char buf[40];
6 name = sat_stack_pop_string_alloc();
7 sprintf(buf,"Hi %s!",name);
8 sat_stack_push_string(buf);
9 return(0);
10 }
This program will take a string from the stack and put it
back on the stack with "Hi " and "!" wrapped around it. In detail:
-
Line 6 will pop the string off the stack, allocate some
memory to hold the string, then return the address of the string in memory
to the character string pointer name
allocated on line 4.
-
Line 7 stores in the character string
buf the contents of the string that
name points to with "Hi " and "!"
wrapped around it.
-
Line 8 pushes the the character string
buf to the stack.
There is no need to clear the screen or wait for input.
Compile this like the previous example and create a standalone executable, then
put a string on the stack and press
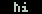 ,
e.g.:
,
e.g.:


Crashes
If you have not already reset your 50g, take your paper clip and reset your
50g using the reset hole on the back of the 50g. Expect to do this
frequently. You should only lose the contents of the stack.
Crashes are usually caused by yours or someone else's bug.
Expect most of them to be your bugs. Crashes are frequent with C mostly
because of the misuse of pointers. In the real world they are called
segmentation faults. To create one simply try to access a region of memory
not assigned to one of your variables. Most CLI workstation programs will
error with some type of useful message, e.g. "Segmentation fault (core dumped)".
HPGCC segfaults return nothing. HPGCC stuck in a loop also returns
nothing. Debugging HPGCC can be a challenge, but a welcome challenge given
the power C brings to the 50g.
To illustrate this take a look at the
hi.c program above, can you spot the
bug? What if name points to a
string longer than 36 characters? buf
is only allocated for 40 characters with 4 being used for "Hi !". Try it.
Put 40 character string on the stack and press
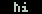 . Make sure
your paper clip is handy. My workstation version of this program returns a
segfault, I suspect HPGCC does too, but is more subtle. Hopefully future
versions of HPGCC will create a core or stack dump on the SD card for analysis.
. Make sure
your paper clip is handy. My workstation version of this program returns a
segfault, I suspect HPGCC does too, but is more subtle. Hopefully future
versions of HPGCC will create a core or stack dump on the SD card for analysis.
Fixing hi.c can be
done a few different ways. E.g., you could take the first 36
characters and discard the rest (35 really since each string must end in '\0'
a.k.a. NULL), or you could dynamically allocate the size of
buf based on the length of
name + 5, or you could reject long
strings.
Hangs
Hangs are not crashes. Hangs are probably stuck in
a loop or waiting for I/O. In the CLI world you send an interrupt (usually
a CTRL-C), but that is not an option with HPGCC. But with a little effort
you can put emergency exits in your code.
E.g., what not to do:
#include <hpgcc49.h>
int main(void)
{
while(1)
;
//never gets here
return(0);
}
The above code will never exit the while loop and you will
be forced to reset.
#include <hpgcc49.h>
int main(void)
{
while(1)
if(keyb_isAnyKeyPressed())
break;
return(0);
}
This code will also loop forever but will exit with any key
press. If you are going to have large iterative loops consider giving
yourself an out. If you are developing code for others consider some sort
of indicator other than the hour glass icon that something is happening so that
they do not prematurely exit loops or hard reset. The Convex Hull example
has an example of a graphical progress bar.
Wrappers
As stated in the introduction; C is not a complete
replacement for UserRPL. UserRPL provides some very powerful tools for
input and stack manipulation that may be more difficult under C. Take forms
for example. They are not going to run any faster under C, so why bother?
There is a correlation between the number of bugs in your code and the
length of the code. IOW, keep it short and simple whenever possible and use the right
tool for the right job. Often a simple wrapper around your C code can make
a big difference, e.g. try using using hi.c
without a string:
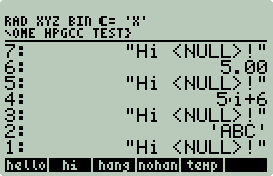
hi.c cannot pop a
string off the stack. NULL is returned and then pushed out as
"Hi <NULL>!". A simple wrapper
like: \<< \->STR hi \>> solves this
problem for almost any case, e.g.:
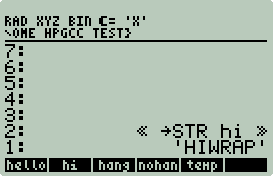
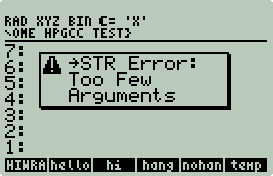

Send nothing and get a
"Too Few Arguments" error, send anything else and it gets converted to
a string first. Coding object type identification and conversion to string in C is possible but more difficult with
little benefit.
Wrappers are also convenient for returning C errors, e.g.
hi2.c:
#include <hpgcc49.h>
int main(void)
{
char *name;
char buf[40];
name = sat_stack_pop_string_alloc();
if(name == NULL) {
sat_stack_push_string("hi2 Error: String expected!");
sat_push_real(1);
}
else {
if(strlen(name) > 35) {
sat_stack_push_string(name);
sat_stack_push_string("hi2 Error: String too long!");
sat_push_real(1);
}
else {
sprintf(buf,"Hi %s!",name);
sat_stack_push_string(buf);
sat_push_real(0);
}
}
return(0);
}
In this improved version,
hi2.c checks for NULL and long strings
and pushes an error message and an error number (1 in this case). If no
error, then push the new string and 0. Note that if the
name string is too long it is pushed
back on the stack to be consistent with other types of 50g errors, i.e. if there
is something wrong with the argument leave it on the stack. This is not
necessary with the NULL check since nothing was popped off the stack.
The new wrapper and errors look like this:



The new wrapper code IF
statement
pops off the 0 or 1 return code, if nonzero the string returned is used by
DOERR to put a nice error message on
the screen. Otherwise, if zero, then END
leaving the string "Hi ... !" on the
stack. This is a nicer solution than blindly converting to a string
before calling hi because you do not
get unexpected results.
Another benefit of wrappers is that it is simple to
create libraries for your newly created collection of C routines. This
will be documented in detail at the end of this section.
Data Types
C is a statically typed language, i.e. variables are
declared by type in advance at compile time. UserRPL is dynamically typed,
i.e. variables are declared and typed at runtime. This static/dynamic
dichotomy can be a challenge when passing data to and from the stack. This
was clearly illustrated above with hi.c.
To further compound the issue UserRPL has many more data types than C.
However, C can use structures to create more types, e.g. a complex number could
be represented as two real numbers.
In this article UserRPL wrappers will be used to
precondition data passed to C programs and to interpret the results. This
is a simple solution to the problem, but not the only solution, e.g. the freely
available HPStack [3] HPGCC library provides C structures and routines to handle
UserRPL data types such as lists, arrays, and complex numbers.
A detailed explanation of C data types, arrays, and
structures is beyond the scope of this article, but it is an important topic
that is discussed at length in any good C book. From a data management
perspective it is good to know how to correlate C and basic UserRPL types and
how much RAM each type takes so that you can budget your memory usage. The
following program will return the number of bytes used for the common C types:
#include <hpgcc49.h>
int main(void) {
clear_screen();
printf("size_t: %d\n",(int)sizeof(size_t));
printf(" char: %d\n",(int)sizeof(char));
printf(" short: %d\n",(int)sizeof(short));
printf(" int: %d\n",(int)sizeof(int));
printf(" long: %d\n",(int)sizeof(long));
printf(" float: %d\n",(int)sizeof(float));
printf("double: %d\n",(int)sizeof(double));
WAIT_CANCEL;
return(0);
}

size_t is used for
pointers and is 4 bytes (32 bits) long, this is expected since the ARM processor
has a 32 bit address space. char
is a single 8 bit character, it can also double as a very short signed or
unsigned integer. Note: C has no string type, an array of characters
is used instead. short,
int, and
long are signed integers.
float and
double are signed reals.
UserRPL integers can be popped and pushed as any C integer
type as long as it will fit. Because the 50g has arbitrary precision (big
num) integer support not all integers can be popped as C integers. If your
C code understands large integers (see Unbounded Spigot, Next Prime example below), then
conversions to and from strings would be necessary.
UserRPL reals can be popped and pushed as C doubles.
Liberal use of the ->NUM function in
wrappers can save a lot of frustration. E.g. 1/2 in exact mode will not be
popped as a real. ->NUM will
convert any number to a real (even integers, symbols, and variables).
C Binaries Are Big, Too Big
If you been following along and compiled/installed all the examples up to this
point, you may have noticed that your amount of free RAM has been significantly reduced, e.g.:
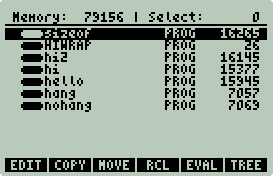
76 KB of RAM has been used for a handful of small examples.
A virgin 50g has less than 241KB available. The solution is simple, do
what others have done since the digital dawn of time, dump it to mass storage.
Create the following UserRPL program and save it as
INSTALL in
home/hpgcc. Next create a Custom
Menu CST variable with the contents
{INSTALL} in the same directory.
%%HP: T(3)A(R)F(.);
\<< \-> p
\<<
p EVAL
p PURGE
S\->EXE
"EXTEND/" p +
3 \->TAG
DUP
PURGE
STO
\>>
\>>
|
 |
This UserRPL program will push to the stack a compiled C
program (but not a standalone), purge it from RAM, convert it to standalone, and
save it to SD as EXTEND/PROGNAME.
If PROGNAME exists, it will be
replaced, and if the EXTEND directory
does not exist, it will be created.
Purge everything from the
home/hpgcc/test directory except
HIWRAP, then transfer
hi2.hp from your workstation to
home/hpgcc/test.
To install press


 .
.
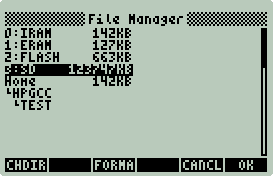
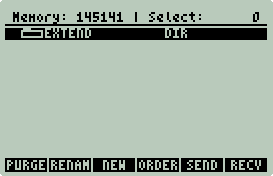
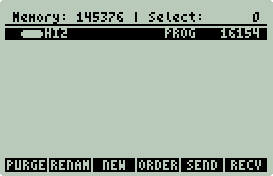
Use the File Manager to examine the SD card. There should
be an EXTEND directory. Within the
EXTEND directory
HI2 should have been
installed.
NOTE: The SD FAT file system has a couple of
restrictions:
-
A file and directory names must be in 8.3 format:
SSSSSSSS.XXX. The extension can
be omitted.
-
Names are not case sensitive. All the examples have
been in lowercase (e.g. hi2.hp).
The .hp gets dropped when transferred
from workstation to 50g. Once saved to SD
hi2 can be recalled as
hi2 or
HI2.
After moving your C binaries to SD all this is required to
execute them is a minor update to the wrappers, e.g. for
HIWRAP:
Old
|
|
New
|
 |
|
 |
Since there is no longer any naming conflict or confusion I
recommend that your wrapper names closely match the C executable name.
Base Template
The above
examples are a good foundation for your own code but are missing an important
feature. Speed. Below is a better template to start with:
#include <hpgcc49.h>
int main(void)
{
//your variables
//optional clear screen for direct text output
//clear_screen();
//full speed ahead
sys_slowOff();
//your critical code here
//back to slow
sys_slowOn();
//optional notify/pause for cancel
//beep();
//WAIT_CANCEL;
return(0);
}
The 50g by default runs at 75 MHz. This is probably a
requirement to get good Saturn emulation performance. HPGCC by default
runs at 12 MHz, but can also run at 75 MHz. I did two different tests
comparing native Saturn code to compiled C code and found that at 12 MHz, HPGCC
was approximately 15 times faster, and at 75 MHz, approximately 90-100 times
faster. There is a performance and battery life trade off you will need to
consider. I speculate that most will want to run at full speed.
The calls
sys_slowOff() and sys_slowOn()
are used to change between 75 MHz and 12 MHz. After declaring all your variables call
sys_slowOff(). This will clock the 50g to max speed and max battery burn. Write your
critical code, then end
with sys_slowOn().
If you decide to pause with
WAIT_CANCEL or any other input request,
I recommend that you call sys_slowOn()
and beep() first. This is
important because the 50g will not auto power off outside of UserRPL.
Perhaps during a lengthy computation you get distracted,
beep() will help you get refocused.
And,
if for some reason you left your 50g unattended at least its back to slow mode
conserving battery power.
In general consider the uses of sys_slowOn(),
sys_slowOff(), and
beep() throughout your code if frequently pausing for
input, e.g. a chess game program. Why burn batteries while you are
thinking?
Extend your 50g with C
To truly extend the 50g you need to create a library.
Once this library is created you can easily share your C programs with others.
In this last introductory example you will create an
Arithmetic Geometric Mean (AGM) function for the 50g. This is an example
of what not to do in C because this function converges very quickly (the UserRPL
version is as fast as the C version), but, it is useful as an example.
agm.c
|
|
AGM UserRPL |
#include <hpgcc49.h>
int main(void){
double a,b,c;
sys_slowOff();
a = sat_pop_real();
b = sat_pop_real();
if(a < 0 || b < 0) {
sat_push_real(a);
sat_push_real(b);
sat_push_real(1);
sys_slowOn();
return(0);
}
while (fabs(a-b) > 1e-10) {
c = a;
a = (a + b)/2;
b = sqrt(b * c);
if(keyb_isAnyKeyPressed())
break;
}
sat_push_real((a+b)/2);
sat_push_real(0);
sys_slowOn();
return(0);
}
|
|
\<< \-> a b
\<<
WHILE a b - ABS .0000000001 >
REPEAT
a b + 2. /
a b * \v/
'b' STO
'a' STO
END
a b + 2. /
\>>
\>>
|
The AGM function takes two reals, computes the AGM, and
returns a single real. AGM approximately doubles in precision after each
iteration. Only four iterations are needed to exhaust the precision of 64
bit (double) floats. However, do not make this assumption, the
while test condition in both programs
depends on the values of a and
b. Certain values of
a and
b have the potential to loop forever. You have a few options to
address this:
-
Give yourself an out. In the C program
keyb_isAnyKeyPressed is used to check
for input and break out of the loop and return intermediate results. Since
UserRPL programs can be interrupted with CANCEL( ),
it is not necessary for the UserRPL version to explicitly check for input.
),
it is not necessary for the UserRPL version to explicitly check for input.
-
Prove mathematically that for any pair of 64 bit floating
point numbers that there will be a small finite number of iterations required to
converge.
-
Hard code the number of loops to four or hard code a
maximum number of iterations. Taking the time to better understand the
mathematical properties of the algorithm can go a long way in space and speed
optimization. This has been critical throughout the ages in calculator
algorithm design--keep with tradition.
Since the sqrt
function cannot take the square root of a negative number it is necessary to
check for negative values, this could have also been done in the wrapper.
Compile and install to SD
agm.c using the previous instructions above. Next create the AGM
wrapper:
%%HP: T(3)A(R)F(.);
\<< "Usage: Input 2 positive reals." \-> u
\<<
|
Define a local variable
u as our universal error message
for UserRPL and C.
|
DEPTH IF 2 < THEN u DOERR END
|
Check for a stack depth less than two, if true,
then put u on the stack, call
DOERR and end (DOERR
implicitly ends the UserRPL program).
|
\->NUM SWAP \->NUM
|
Convert the first two stack elements to reals
using ->NUM.
->NUM is very handy to precondition
input for C programs. ->NUM
never errors if it cannot convert to a real. And
->NUM will convert symbolic inputs
to reals (e.g.
 ). ).
|
DUP2 TYPE SWAP TYPE +
|
Duplicates the two stack items, and sums their
type values.
|
IF THEN u DOERR END
|
The type for reals is 0, if the sum is not 0,
then put u on the stack and call
DOERR.
|
:3: "EXTEND/AGM" EVAL
|
If you got this far you have 2 reals on the
stack, call EXTEND/AGM.
|
IF THEN u DOERR END
\>>
\>>
|
Check for nonzero return code, if nonzero, then
u DOERR.
agm.c only returns 1 if a or b is
negative. agm.c also pushes a
and b back on stack to be consistent with other 50g errors, i.e. the values
that causes the error are left on the stack. |
Non-annotated version:
%%HP: T(3)A(R)F(.);
\<< "Usage: Input 2 positive reals." \-> u
\<<
DEPTH
IF 2 < THEN u DOERR END
\->NUM SWAP \->NUM
DUP2 TYPE SWAP TYPE +
IF THEN u DOERR END
:3: "EXTEND/AGM" EVAL
IF THEN u DOERR END
\>>
\>>
Why not use C to do all of this?
-
Library needs a wrapper.
-
Currently the HPGCC code to validate reals on the stack is
broken.
-
More work to convert symbolic numbers (e.g.
 ).
).
-
No performance benefit.
-
Could make C code longer and buggier.
I recommend that libraries for C programs only contain the
wrappers and not the C executables. Libraries are stored in ports 1 or 2.
Both have limited space.
To create a library first define and store the following
variables (yes the $ (
 in ALPHA mode) is part of the
variable name):
in ALPHA mode) is part of the
variable name):
Variable
|
|
Value |
|
Description |
$TITLE
|
|
"EXTEND" |
|
This is the title of the library. The first five
characters will be used for the name that is shown in the library menu.
|
$ROMID
|
|
1313 |
|
This is a number (real or integer) which must be unique
to your library. This allows the calculator to identify the library, and
should be in the range 769 to 1792.
|
$CONFIG
|
|
1 |
|
Default configuration.
|
$VISIBLE
|
|
{AGM} |
|
This is a list of the commands in the current directory
that you want to have in the library and visible in the library's menu. |
Your home/hpgcc/test
should look like this:

To create the library and store (not install) to SD card
type into the 50g:
256 ATTACH

CRLIB

:3:EXTEND.LIB

Your stack should look like this:

Save to SD Card by pressing
 .
Your SD card now has an EXTEND
directory and an EXTEND.LIB file.
If you wish to share your C code and wrappers then just zip up both
EXTEND and
EXTEND.LIB as
EXTEND.ZIP and distribute. The
installation instructions are very simple (you can skip 1 and 2 since you
already have it on your 50g):
.
Your SD card now has an EXTEND
directory and an EXTEND.LIB file.
If you wish to share your C code and wrappers then just zip up both
EXTEND and
EXTEND.LIB as
EXTEND.ZIP and distribute. The
installation instructions are very simple (you can skip 1 and 2 since you
already have it on your 50g):
-
On your PC extract
EXTEND.ZIP into the root of the SD Card.
-
Insert SD Card into 50g.
-
Type into the 50g:
:3:EXTEND.LIB


2


Now press
 ,
then press
,
then press  +
+ .
.
-
Test. Try a few pairs of numbers, try negative
numbers, try symbolics, try variables.
Congratulations you just added
AGM to the 50g vocabulary. If you
like, you can remove the HOME/HPGCC/TEST
50g directory, it is not needed to run AGM.
If you enter 1313 MENU in your 50g you
can see all new commands this library adds.
The Computational Geometry section has a larger example
including how to add an entry to the APPS
menu.
Debugging
Debugging C code is always a challenge with the proper
tools and a real challenge without them. HPGCC includes no traditional
debuggers (e.g. GDB). Actually HPGCC does include the original early 80's
debugger: printf. If you
are not laughing then you are new to C.
Debugging Options:
-
Prototype on workstation first. That's the beauty of
C, it runs on anything. Algorithm design, file I/O, etc... can be tested
on your workstation first, then ported to the 50g limiting the debugging to HPGCC
bugs.
-
printf.
Print state information to the screen, this has been a tried and true method of
debugging ever since computers could output to printer or screen.
-
fprintf.
File printf. You can put a lot of
information in a file for analysis on your workstation.
-
Use the HPAPINE simulator[4]. This tool can really
speed up development and testing. It cannot debug all HPGCC bugs, but it
can catch most of them, and, since it runs on your workstation, tools like GDB are
available.
HPAPINE 101
HPAPINE is an implementation of the
HPGCC's API. Usually, a
HP49g+/50g program written in C is compiled by HPGCC. With HPAPINE, you can
compile the same program so that it runs natively on your Unix system. [4]
HPAPINE prebuilt for Cygwin/X, Linux, and OS/X is included as part of the
hpgcc.tgz,
hpgcc-linux.tgz, and
hpgcc-osx.tgz tarballs.
NOTE: XP users must have SP2 or later
installed to build HPAPINE binaries.
To give HPAPINE a test drive type the following in a new
Xterm session:
cd ~/hpgcc/test
make clean
make hello_local
make agm_local
Your session should look something like this (inputs are in
bold):
$ cd ~/hpgcc/test
$ make clean
rm -f *.o
rm -f *.hp
rm -f *.exe
$ make hello_local
gcc -Wall -g -o hello_local hello.c -DHPGCC -I ~/hpgcc/2.0SP2-hpapine/include/ \
-DHPAPINE -L ~/hpgcc/2.0SP2-hpapine/lib/ -lhpapine \
-L/usr/X11R6/lib -lgdk-x11-2.0 -lgthread-2.0 -lgdk_pixbuf-2.0 -lpangoxft-1.0 \
-lXft -lfreetype -lz -lXrender -lXext -lfontconfig -lpangox-1.0 -lX11 \
-lpango-1.0 -lm -lgobject-2.0 -lgmodule-2.0 -lglib-2.0 -lintl -liconv
$ make agm_local
gcc -Wall -g -o agm_local agm.c -DHPGCC -I ~/hpgcc/2.0SP2-hpapine/include/ \
-DHPAPINE -L ~/hpgcc/2.0SP2-hpapine/lib/ -lhpapine \
-L/usr/X11R6/lib -lgdk-x11-2.0 -lgthread-2.0 -lgdk_pixbuf-2.0 -lpangoxft-1.0 \
-lXft -lfreetype -lz -lXrender -lXext -lfontconfig -lpangox-1.0 -lX11 \
-lpango-1.0 -lm -lgobject-2.0 -lgmodule-2.0 -lglib-2.0 -lintl -liconv
Now run run hello_local.
Session output (inputs are in bold):
$ ./hello_local
HPAPINE version 20071113_134757 (HPGCC 2.0)
Compiled on Sat Dec 8 18:45:20 MST 2007
CYGWIN_NT-5.1 1.5.24(0.156/4/2) i686 (oberon)
STRICT_HPGCC: no
GUI: GDK (X11)
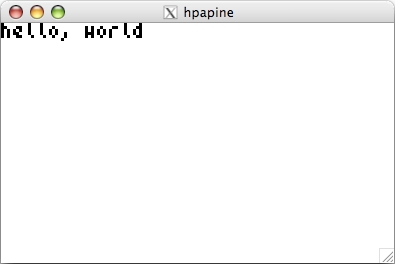
A new window will pop up with the simulated 50g output:
This window is identical to the what was displayed on the
50g. If you still have hello.hp
installed on your 50g see for yourself. Interacting with this window is
identical to interacting with the 50g. The letters on your keyboard match
up with the numeric, math operator, and alpha keys from the 50g.
 is
simulated with <ESC>. Press
<ESC> now to exit the application.
is
simulated with <ESC>. Press
<ESC> now to exit the application.
HPAPINE can also simulate the stack for input and output
from 50g programs. To see how this works run
agm_local. Session output (inputs
are in bold):
$ ./agm_local
HPAPINE version 20071113_134757 (HPGCC 2.0)
Compiled on Sat Dec 8 18:45:20 MST 2007
CYGWIN_NT-5.1 1.5.24(0.156/4/2) i686 (oberon)
STRICT_HPGCC: no
GUI: GDK (X11)
--- Waiting for stack input on stdin...
1.456
7.4563
--- Stack reading: done.
--- RPL Stack:
2: 1.456
1: 7.4563
HPAPINE version 20071113_134757 (HPGCC 2.0)
Compiled on Sat Dec 8 18:45:20 MST 2007
CYGWIN_NT-5.1 1.5.24(0.156/4/2) i686 (oberon)
STRICT_HPGCC: no
GUI: GDK (X11)
--- RPL Stack:
2: " 3.85362"
1: " 0"
This is exactly what the 50g would have returned without
the wrapper. The result in stack position 2 is our answer (verify on your
50g), and the 0 in position 1 was the return code. NOTE: When
entering values into the stack, enter them as if you were using a 50g, to
terminate entry and continue running the application use
<Ctrl-D>.
Next try using GDB and
hello_local. Session output (inputs are in bold):
$ gdb hello_local
GNU gdb 6.5.50.20060706-cvs (cygwin-special)
Copyright (C) 2006 Free Software Foundation, Inc.
GDB is free software, covered by the GNU General Public License, and you are
welcome to change it and/or distribute copies of it under certain conditions.
Type "show copying" to see the conditions.
There is absolutely no warranty for GDB. Type "show warranty" for details.
This GDB was configured as "i686-pc-cygwin"...
(gdb) start
Breakpoint 1 at 0x401075: file hello.c, line 4.
Starting program: /cygdrive/c/home/egan/hpgcc/test/hello_local.exe
Loaded symbols for /cygdrive/c/WINDOWS/system32/ntdll.dll
...
Loaded symbols for /usr/bin/cyggthread-2.0-0.dll
main ()
at hello.c:4
4 {At this point GDB displays the next line to be executed.
Use 'n<Enter>' to step through GDB.(gdb) n
5 clear_screen();
(gdb) n
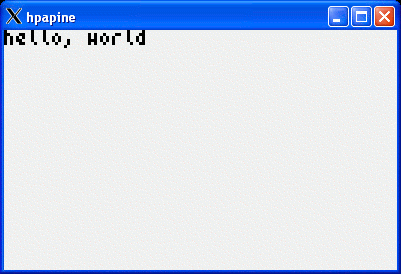
After
clear_screen(); executes a blank hpapine window pops up:
6 printf("hello, world\n");
(gdb) n
7 WAIT_CANCEL;
(gdb) n
You'll notice the GDB does not return a (gdb)
prompt, it is waiting for program input. Press
<ESC> in the hpapine window.8 return(0);
(gdb) n
9 }
(gdb) n
0x61006198 in dll_crt0_1 () from /usr/bin/cygwin1.dll
(gdb) n
Single stepping until exit from function _Z10dll_crt0_1Pv,
which has no line number information.
HPAPINE version 20071113_134757 (HPGCC 2.0)
Compiled on Sat Dec 8 18:45:20 MST 2007
CYGWIN_NT-5.1 1.5.24(0.156/4/2) i686 (oberon)
STRICT_HPGCC: no
GUI: GDK (X11)
Program exited normally.
(gdb) q
Great stuff! For more information on GDB read:
http://sourceware.org/gdb/current/onlinedocs/gdb.pdf.gz.
Just a few warnings about HPAPINE:
-
It is alpha level code.
-
Sometimes code works with HPAPINE but does not work on the 50g.
-
Sometimes code works with the 50g but not HPAPINE.
-
The stack output can be a bit twitchy.
-
Some libraries may not have HPAPINE support (e.g. win,
hpstack) and may need to be compiled or not used.
You mileage may vary. I will state that HPAPINE has
saved me hours and hours of work when developing HPGCC applications.
Use it.
Makefiles
Makefiles are plain text files with instructions on how to
make something. All of the Makefiles in this article have been
created for you. The easiest way to create a Makefile is to copy it from
another source and modify it. The
Makefile in ~/hpgcc/test is a
Makefile I modified from the HPGCC distribution. This Makefile is all you
need if you are developing single source file binaries using only HPGCC supplied
libraries.
E.g. lets say you wrote the program
foo.c. To compile it for the 50g
you would copy foo.c to
~/hpgcc/test and then type:
$ make foo.hp
arm-elf-gcc -mtune=arm920t
-mcpu=arm920t -mlittle-endian -fomit-frame-pointer -msoft-float -Wall -Os
-I/home/egan/hpgcc/2.0SP2/include -L/home/egan/hpgcc/2.0SP2/lib -mthumb-interwork
-mthumb -c hello.c
arm-elf-ld -L/home/egan/hpgcc/2.0SP2/lib -T VCld.script /home/egan/hpgcc/2.0SP2/lib/crt0.o
hello.o -lhpg -lhplib -lgcc -o foo.exe
elf2hp -s3000 foo.exe foo.hp
rm foo.o foo.exe
Say you wanted to test it first with HPAPINE, then type:
$ make foo_local
gcc -Wall -g -o foo_local
foo.c -DHPGCC -I /cygdrive/c/home/egan/hpgcc/2.0SP2-hpapine/include/ \
-DHPAPINE -L /cygdrive/c/home/egan/hpgcc/2.0SP2-hpapine/lib/ -lhpapine \
-L/usr/X11R6/lib -lgdk-x11-2.0 -lgthread-2.0 -lgdk_pixbuf-2.0 -lpangoxft-1.0 -lXft
-lfreetype -lz -lXrender -lXext -lfontconfig -lpangox-1.0 -lX11 -lpango-1.0 -lm
-lgobject-2.0 -lgmodule-2.0 -lglib-2.0 -lintl -liconv
Throughout this article I will start with this Makefile and
modify it as needed. I will comment on the changes. For detailed
information about Makefiles consider reading Managing Projects with make
by Oram and Talbott.
Support
You are not alone. There are a few avenues for
support:
-
Read the HPGCC documentation:
-
cd ~/hpgcc/2.0SP2/doc_html
-
cd into
decNumber,
fsystem,
ggl,
hpg, hplib, or
win
-
Load index.html
into any browser.
-
The official HPGCC home page:
http://hpgcc.org.
-
The official HPGCC mailing list. To subscribe go to
https://lists.sourceforge.net/lists/listinfo/hpgcc-devel. To read the
archives go to
http://sourceforge.net/mailarchive/forum.php?forum_name=hpgcc-devel.
-
Search first, then post to the
Usenet group comp.sys.hp48.
If you do not have an NNTP reader and account you can search and post freely
here:
http://groups.google.com/group/comp.sys.hp48/topics.
-
A bunch of helpful and friendly calculator nerds can be
found here:
http://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/forum.cgi. Go to
http://www.cafepress.com and search for
calculator if you want to see what these nerds wear. You may spot one in
the wild. If you do, approach slowly, make no sudden movements, then
politely ask for help.
-
Google.
-
Use the source. HPGCC is free as is free
beer and free speech.
Summary
Hopefully you have enough information to be dangerous and
possibility productive. Where do you go from here? I would suggest
that you start by looking other people code. The
~/hpgcc/2.0SP2/examples directory on
your system has a lot of great examples. The 2nd half of this article has
more complex examples involving the use of existing open source C libraries and
source code.
Good luck!
Extend your 50g with C - Part 2
Part one of this article assumes little to no knowledge of HPGCC
and C. This section will focus on learning by example by
illustrating how to create complete mathematical extensions to the 50g.
The reader is assumed to know how to compile C code with HPGCC, install binaries to SD, and create wrappers.
All of this
was covered in Part 1.
How to Follow the Examples
-
All binaries should be installed on the SD Card in the
EXTEND directory.
-
$ prompts indicate
something you should type. The text to be entered will be in
bold courier and the output in
courier, e.g.:
$ hello
go away!
-
All the code is in the ~/hpgcc
directory. Each example has it's own subdirectory. Files ending in
.c.nl are line numbered version of the
.c code. My comments will
reference line numbers. Line numbers were generated with:
perl -pi -e 's/\t/
/g' < program.c | nl -nln -ba >program.c.nl
-
All C programs will be in lowercase courier, e.g.
program. All RPL wrappers will be
in uppercase courier, e.g. PROGRAM.
-
To maintain consistency most code was reformatted with:
indent -kr -ts4 *.c *.h
The Examples
-
Real and Complex LogGamma. This is an example
of how to do complex operations in C. C, unlike C99, C++, and Fortran, has
no native support for complex numbers. Furthermore, LogGamma is its own
function and is not exactly the same as the 50g ln(gamma()).
-
Sparse Linear Solver. This is an example of a
very fast sparse linear solver capable of solving sparse systems too large for
the 50g internal dense linear solver. This example will also demonstrate
how to work with lists and arrays.
-
π Shootout. This example adds no immediate
benefit to the 50g, but its fun. This example illustrates how to use an
arbitrary multiple precision math library and a large integer math library.
This example will also demonstrate how to work with files and text screen
output.
-
Computational Geometry Library. This is an
example of how to create static and interactive CG applications from freely
available CG C code (e.g., convex hull (10,000 points in
seconds), Voronoi diagrams, etc...). This
example will also demonstrate how to take screen shots (B&W and grayscale).
This example ends by creating a redistributable CG library with
an APPS menu.
Example: Real and Complex LogGamma
You might be asking yourself, "Why not use the built in 50g functions
ln() and
gamma() together to compute
LogGamma()?"
There are two reasons:
-
ln(gamma(z)) is not exactly the same
as LogGamma(z). E.g.:
ln(gamma(12.3+4.56i)) = 17.38 - 1.20i
whereas
LogGamma(12.3+4.56i) = 17.38 + 11.36i
A difference of 2πn where n = 2. Since ln(z)
= ln|z| + iarg(z), and arg(z) is in the interval [-π,π), the
imaginary part will always be mod 2π. IOW,
ln(gamma(z)) and
LogGamma(z) have different branch cut structures. Refer to [5]
for details.
-
Because LogGamma() is its own function and not the combination
of ln() and
gamma() large values for
z can be computed. E.g. 50g
ln(gamma(500)) = 1151.29, whereas
LogGamma(500) = 2605.12. Any value
greater than 254 on the 50g will always return 1151.29.
The HPGCC working directory for this example is in
~/hpgcc/complex. The 50g working
directory is assume to be HOME/HPGCC/COMPLEX.
Building c9x-complex
Unfortunately HPGCC C has no native support for complex
numbers. Fortunately there are freely available complex C libraries.
The c9x-complex library is very complete and includes a
LogGamma() function.
99% of the work is already done!
-
Change to working directory:
$ cd ~/hpgcc/complex
-
Download and extract
c9x-complex.tgz:
$ wget http://www.moshier.net/c9x-complex.tgz
$
tar zxvf c9x-complex.tgz
-
Create stubs. This is something that you will do
frequently. You have two choices, you can edit every file and change
stdio.h and possibly other files to
hpgcc49.h or you can create your own
stdio.h that includes
hpgcc49.h. The second method is
preferred. It is best to alter the code as little as possible so that you
can benefit from updates and get more support from the authors and the community.
$ cd c9x-complex
$
mkdir stubs
$
echo '#include <hpgcc49.h>' >stubs/stdio.h
-
Create ~/hpgcc/complex/c9x-complex/Makefile.hpgcc.
This is a hybrid of a standard HPGCC Makefile and the Makefile included with
c9x-complex. By examining both Makefiles you can see that most of the
differences are in the compiler and compiler flag settings. Also notice
the -Istubs added to the standard HPGCC
CFLAGS. When
stdio.h is encounter by the C
preprocessor it will search and find stubs/stdio.h
and include that. That will then include
hpgcc49.h.
INCLUDE_PATH= $(HPGCC)/include
CC= arm-elf-gcc
AR= arm-elf-ar
RANLIB= arm-elf-ranlib
CFLAGS= -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I. -Istubs -mthumb-interwork -mthumb
DFILES = cmplx.o clog.o cgamma.o
LIBMCFILES = $(DFILES) stubs.o
all: libmc.a
libmc.a: $(LIBMCFILES)
rm -f libmc.a
$(AR) cr libmc.a $(LIBMCFILES)
$(RANLIB) libmc.a
clean:
rm -f *.o
rm -f libmc.a
- Make it:
$ make -f Makefile.hpgcc clean
rm -f *.o
rm -f libmc.a
$ make -f Makefile.hpgcc
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o cmplx.o cmplx.c
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o clog.o clog.c
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o cgamma.o cgamma.c
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o stubs.o stubs.c
In file included from mconf.h:177,
from stubs.c:5:
protos.h:85: error: expected ')' before '/' token
make: *** [stubs.o] Error 1
Doh! What's this hard to understand error? Line 85 in
protos.h doesn't look out of the
ordinary:
extern double log2 ( double x );
What's up? Well, log2 conflicts with
the log2 macro in
hpmath.h:
#define log2(x) (log(x) / M_LOG2_E)
One or the other has to yield. For now, just comment out line 85 in the
protos.h with
// and try to make again:
$ make -f Makefile.hpgcc
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o cmplx.o cmplx.c
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o clog.o clog.c
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o cgamma.o cgamma.c
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I. -Istubs -mthumb-interwork
-mthumb -c -o stubs.o stubs.c
rm -f libmc.a
arm-elf-ar cr libmc.a cmplx.o clog.o cgamma.o stubs.o
arm-elf-ranlib libmc.a
c9x-complex is now built.
Get a Complete libm.a
The math library in HPGCC is missing a few
things. Fortunately Jean-Yves Avenard has built us a
proper libm.a.
All that is needed is to extract it and link with it.
-
Change to working directory:
$ cd ~/hpgcc/complex
-
Obtain JYA toolchain:
$ wget
http://www.hydrix.com/Download/Hp/hpgcc/arm-elf-toolchain.4.2.2.linux.tar.bz2
-
Extract libm.a
$ tar jxvf arm-elf-toolchain.4.2.2.linux.tar.bz2
/opt/arm-hp/arm-elf/lib/thumb/interwork/libm.a
$ cp opt/arm-hp/arm-elf/lib/thumb/interwork/libm.a .
-
Clean up:
$ rm -r ./opt arm-elf-toolchain.4.2.2.linux.tar.bz2
LogGamma
With libmc.a and
libm.a in hand implementing a fast Complex LogGamma
for the 50g is relatively easy in 29 lines of code:
1 #include <hpgcc49.h>
2 #include <complex.h>
3
4 int __errno;
5
6 int main(void) {
7 double r,i;
8 double complex w,z;
9
10 sys_slowOff();
11
12 i = sat_pop_real();
13 r = sat_pop_real();
14
15 if(i == 0 && (r == 1 || r == 2)) {
16 sat_push_real(0);
17 sat_push_real(0);
18 }
19 else {
20 z = r + i * I;
21 w = clgam(z);
22
23 sat_push_real(creal(w));
24 sat_push_real(cimag(w));
25 }
26
27 sys_slowOn();
28 return (0);
29 }
-
Lines 2 and 4 add the declarations required by the c9x-complex and standard
math libraries.
-
Line 8 defines 2 complex variables.
-
Lines 12 and 13 pop off 2 reals from the stack. HPGCC
does not have native support for popping off a complex number. An even if
it could, you still have the complexities of making sure both parts are reals
and not symbolic. This is best left to the wrapper.
-
Lines 15-18 check for some known values that should return
0, but that clgam() returns as very
small reals.
-
Lines 20 and 21 is where the magic happens.
-
Lines 23 and 24 push the real and imaginary values to the
stack to be processed by the wrapper.
Makefile
The Makefile for LogGamma is the same used in Part 1 with the following changes
in bold:
export C_FLAGS= -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -Ic9x-complex -L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD= arm-elf-ld
export LD_FLAGS= -L$(LIBS_PATH) -Lc9x-complex -L. -T VCld.script $(LIBS_PATH)/crt0.o
export LIBS= -lmc -lm -lhpg -lhplib -lgcc
-
-Ic9x-complex tells the C
processor to also look for include files in the directory
c9x-complex. This is where
complex.h exists.
-
-Lc9x-complex -L. tells the
linker to look also look for libraries in the
c9x-complex and current directory.
-
-lmc -lm tells the linker to link in
libmc.a and
libm.a. The order of the
libraries is important. If two libraries share a common function, the
first one listed gets used. If a library relies on functions in another
library, then the library that provides the specific function must be placed
after the library requesting the functions. IOW,
libmc.a needs functions from
libm.a and all libraries need base
functions from libgcc.a.
To build it type:
make clean
make loggamma.hp
Wrapper
loggamma UserRPL wrapper:
%%HP: T(3)A(R)F(.);
\<< \->NUM DUP TYPE
IF 1 ==
THEN
C\->R
ELSE
0.
END
:3: "EXTEND/LOGGAMMA" EVAL
DUP
IF 0 ==
THEN
DROP
ELSE
R\->C
END
\>>
This wrapper starts out by converting the input to a number, duplicating it,
then converting the duplicate to its type. If type 1 (complex number),
then breakout the number into is real and imaginary components, otherwise put a
0 on the stack as the imaginary part. Up to this point all that has been
done is to insure that there is a complex number Re and Im on the stack in that
order.
Next, extend/loggamma is executed and returns to the stack a complex number as Re and Im as two stack elements.
The Im is duplicated to preserve its value and checked for 0. If 0 the
value is dropped and the wrapper ends with a real (Re) result, otherwise the two
reals (Re and Im) are combined as a type 1 complex number on the stack.
LogGamma Test
z
|
ln Γ(z)
|
50g loggamma(z)
|
50g ln(gamma(z))
|
|
1 |
0 |
0 |
0 |
|
100 |
359.134205370 |
359.13420537 |
359.13420537 |
|
1000 |
5905.22042321 |
5905.22042321 |
1151.2925465 |
|
5555.4444 |
42343.2 |
42343.1698379 |
1151.2925465 |
|
12+34i |
-11.7232 + 102.052i |
(-11.7232,102.0521) |
(-11.7232,1.5212) |
Incorrect answers in bold.
Summary
You now have everything you need to create single source complex number C binaries
for your 50g. Just copy them in ~/hpgcc/complex
and type make.
Example: Sparse Linear Solver
Inspiration for this example came from the following
challenge:
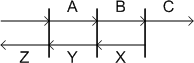
"Three panes of glass are arranged parallel to each
other. Each pane allows 70% light through, reflects 20%, and absorbs 10%.
What percentage of light will pass entirely through all panes of glass?
Assume a beam of light is emitted to the left of the three panes and exits to
the far right; how much emits out to the right?" --
http://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/archv017.cgi?read=118862
Constants:
T = 0.7
(light through)
R = 0.2
(light reflected)
The solution (C) to this problem can easily be
obtained from the following system of equations:
|
A = T + R*Y
|
Initial light through + reflected Y light. |
|
B = T*A +
R*X
|
A light through + reflected X light. |
|
C = T*B
|
B light through. |
|
Y = T*X +
R*A
|
X light through + reflected A light. |
|
X = R*B
|
Reflected B light. |
The above 5 equations can also be represented
by the following sparse linear system:
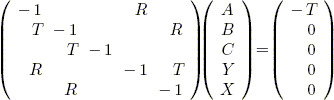
Solving for C with 3 panes is simple, just put
it in your 50g. But what about 4 panes or 100? That was the question
I asked myself when I first read this challenge. The solution to the 4 panes problem is similar.
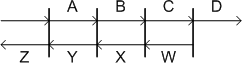
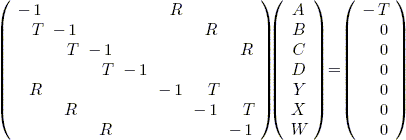
But, what about 100? Clearly there is a pattern that can be generated for any
number of panes. The following RPL program will generate a coefficient
matrix and constant term vector for any number of panes based on this pattern.
Dense Panes (DPANES):
%%HP: T(3)A(R)F(.);
\<< 0. \-> t r n m @ Get T, R, and N from stack
\<<
n 2 * 1 - 'm' STO @ Compute M (matrix size)
t NEG 0 m 1 - NDUPN 1 + \->ARRY @ Create constant term vector
-1 m NDUPN \->ARRY { m m } DIAG\-> @ Create -1 diagonal coefficient matrix
n 1 + m FOR i @ Add R elements to diagonal coefficient matrix
i n - i 2 \->LIST r PUT
i i n - 2 \->LIST r PUT
NEXT
1 n 1 - FOR i @ Add T elements to diagonal coefficient matrix
i 1 + i 2 \->LIST t PUT
NEXT
n 1 + m 1 - FOR i
i i 1 + 2 \->LIST t PUT
NEXT
\>>
\>>
To solve using the 50g dense linear solver press
/ then
n GET for the answer, e.g.:
Dense Panes Solver (DPS):
%%HP: T(3)A(R)F(.);
\<< \-> t r n
\<<
t r n DPANES
/ n GET
\>>
\>>
DPS can be used to
solve this problem for any (small) N.
The following table was constructed with output from
DPANES/DPS:
| N |
DPS(.7,.2,N)
|
Coeff. Bytes
16*(2*N)-1)^2
|
Non-Zero
Bytes
16*6*(N-1) |
Zeros
Bytes
16*(4*N^2-10*N+7) |
Time(s)
Setup |
Time(s)
Solve |
| 3 |
38.0266075388% |
400 |
192 |
208 |
0.38 |
0.17 |
| 4 |
28.6686567164% |
784 |
288 |
496 |
0.45 |
0.33 |
| 10 |
5.6721177756% |
5776 |
864 |
4912 |
1.31 |
1.91 |
| 20 |
.3945314511% |
24336 |
1824 |
22512 |
3.96 |
7.98 |
| 30 |
.0274666640% |
55696 |
2784 |
52912 |
8.24 |
20.10 |
| 40 |
.0019121946% |
99856 |
3744 |
96112 |
15.95 |
36.60 |
| 50 |
.0001331246% |
156816 |
4704 |
152112 |
30.67 |
59.42 |
| 100 |
|
633616 |
9504 |
624112 |
|
|
| 200 |
|
2547216 |
19104 |
2528112 |
|
|
| 300 |
|
5740816 |
28704 |
5712112 |
|
|
The size of the coefficient matrix is
((2*N)-1)2. Each matrix element
(including zeros) uses 8 bytes. However, since all the 50g matrix
operations are nondestructive a copy is used doubling the amount of RAM required
(i.e. 16 bytes/matrix element). No other overhead (constant term
vector, scalars, or program code) is being reported.
There is not enough
memory in the 50g to solve N=100,
N=200 or
N=300 because of the large amount of
RAM required to store 39007, 158007, and 357007 zeros respectively. It
should be obvious that using the internal matrix operations to solve this
problem will be memory starved not far beyond N=50. Speed is an issue as well. Consider the number of
unnecessary operations involving zero using a dense linear solver.
The solution to both problems is a sparse linear solver.
Sparse matrix operations vs. dense matrix operations on a sparse linear system
have the following advantages:
-
Setup time will
be reduced by creating an unordered list of triplets. Every
PUT statement in
DPANES requires a matrix copy.
This is slow and reduces the amount of useful RAM by half.
-
Sparse matrix operations handle zeros intelligently.
This increases speed and reduces memory overhead.
-
The sparse matrix operations in this example are
destructive. No copy required. This also increases speed and reduces
memory overhead.
CSparse Library
After a bit of Googling I selected CSparse [6] for this
example. CSparse is very small, very fast, and very portable. Perfect for
embedded programming.
"CSPARSE is a library of C routines which implement a number
of direct methods for sparse linear systems.
The algorithms contained in CSPARSE have been chosen with five
goals in mind:
- they must embody much of the theory behind sparse matrix algorithms,
- they must be either asymptotically optimal in their run time and memory
usage or be fast in practice,
- they must be concise so as to be easily understood and short enough to
print in the book,
- they must cover a wide spectrum of matrix operations,
- they must be accurate and robust." --
http://www.cise.ufl.edu/research/sparse/CSparse/
Building CSparse for the 50g is fairly straight forward:
-
Change to working directory:
$ cd ~/hpgcc/sparse
-
Download and extract CSparse.tar.gz:
$ wget http://www.cise.ufl.edu/research/sparse/CSparse/CSparse.tar.gz
$ tar zxvf CSparse.tar.gz
-
Create stubs. See the LogGamma example for an explanation
as to why this is necessary.
$ cd ~/hpgcc/sparse/CSparse/Lib/
$ mkdir stubs
$
echo '#include <hpgcc49.h>' >stubs/stdio.h
$
echo '#include <hpgcc49.h>' >stubs/stdlib.h
$
echo '#include <hpgcc49.h>' >stubs/math.h
$
echo '#include <hpgcc49.h>' >stubs/limits.h
-
Create ~/hpgcc/sparse/CSparse/Lib/Makefile.hpgcc.
This is a hybrid of a standard HPGCC Makefile and the Makefile included with
CSparse. By examining both Makefiles you can see that most of the
differences are in the compiler and compiler flag settings.
INCLUDE_PATH= $(HPGCC)/include
export CC= arm-elf-gcc
export AR= arm-elf-ar cr
export RANLIB= arm-elf-ranlib
export CFLAGS= -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I../Include -Istubs -mthumb-interwork -mthumb
all: libcsparse.a
CS = cs_add.o cs_amd.o cs_chol.o cs_cholsol.o cs_counts.o cs_cumsum.o \
cs_droptol.o cs_dropzeros.o cs_dupl.o cs_entry.o \
cs_etree.o cs_fkeep.o cs_gaxpy.o cs_happly.o cs_house.o cs_ipvec.o \
cs_lsolve.o cs_ltsolve.o cs_lu.o cs_lusol.o cs_util.o cs_multiply.o \
cs_permute.o cs_pinv.o cs_post.o cs_pvec.o cs_qr.o cs_qrsol.o \
cs_scatter.o cs_schol.o cs_sqr.o cs_symperm.o cs_tdfs.o cs_malloc.o \
cs_transpose.o cs_compress.o cs_usolve.o cs_utsolve.o cs_scc.o \
cs_maxtrans.o cs_dmperm.o cs_updown.o cs_print.o cs_norm.o cs_load.o \
cs_dfs.o cs_reach.o cs_spsolve.o cs_ereach.o cs_leaf.o cs_randperm.o
$(CS): ../Include/cs.h Makefile
%.o: ../Source/%.c ../Include/cs.h
$(CC) $(CFLAGS) -c $<
libcsparse.a: $(CS)
$(AR) libcsparse.a $(CS)
$(RANLIB) libcsparse.a
clean:
rm -f *.o
purge: distclean
distclean: clean
rm -f *.a
- Make it:
$ cd ~/hpgcc/sparse/CSparse/Lib/
$ make -f Makefile.hpgcc distclean
rm -f *.o
rm -f *.a
$ make -f Makefile.hpgcc
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I../Include -Istubs
-mthumb-interwork -mthumb -c ../Source/cs_add.c
...
arm-elf-gcc -mtune=arm920t -mcpu=arm920t -mlittle-endian -fomit-frame-pointer
-msoft-float -Wall -Os -I/home/egan/hpgcc/2.0SP2/include -I../Include -Istubs
-mthumb-interwork -mthumb -c ../Source/cs_randperm.c
arm-elf-ar cr libcsparse.a cs_add.o cs_amd.o cs_chol.o cs_cholsol.o
cs_counts.o cs_cumsum.o cs_droptol.o cs_dropzeros.o cs_dupl.o cs_entry.o
cs_etree.o cs_fkeep.o cs_gaxpy.o cs_happly.o cs_house.o cs_ipvec.o cs_lsolve.o
cs_ltsolve.o cs_lu.o cs_lusol.o cs_util.o cs_multiply.o cs_permute.o cs_pinv.o
cs_post.o cs_pvec.o cs_qr.o cs_qrsol.o cs_scatter.o cs_schol.o cs_sqr.o
cs_symperm.o cs_tdfs.o cs_malloc.o cs_transpose.o cs_compress.o cs_usolve.o
cs_utsolve.o cs_scc.o cs_maxtrans.o cs_dmperm.o cs_updown.o cs_print.o
cs_norm.o cs_load.o cs_dfs.o cs_reach.o cs_spsolve.o cs_ereach.o cs_leaf.o
cs_randperm.o
arm-elf-ranlib libcsparse.a
libcsparse.a is now built.
Easy!
CSparse Front-end
CSparse is a library that cannot be called directly from RPL, a
front-end must be created to take options and data from the stack to pass to
CSparse.
1 #include <hpgcc49.h>
2 #include <cs.h>
3
4 double *load_vector(char *);
5 cs *load_matrix(char *);
6
7 int main (void)
8 {
9 cs *A;
10 double *b;
11 int ok = 0;
12 char *s, *t, *c;
13 int lusol, qrsol, cholsol, return_vector;
14
15 lusol = qrsol = cholsol = return_vector = 0;
16
17 c = sat_stack_pop_string_alloc();
18
19 if(strcmp(c,"LUSOL") == 0)
20 lusol = 1;
21 else if(strcmp(c,"QRSOL") == 0)
22 qrsol = 1;
23 else if(strcmp(c,"CHOLSOL") == 0)
24 cholsol = 1;
25 else {
26 char error[40];
27 char opt[20];
28
29 strncpy(opt,c,19);
30 opt[19] = '\0';
31 sprintf(error,"Unknown option: %s",opt);
32 sat_stack_push_string(error);
33 sat_push_real(1);
34 return(0);
35 }
- Line 2 includes the CSparse header.
- This front-end is a skeleton
for a generic interface to CSparse. The first stack argument is the
CSparse command. Line 17 pops this command string off the stack with
sat_stack_pop_string_alloc().
This function will dynamically allocate enough bytes to store the popped
string and return a pointer to the string or NULL if it failed to allocate
enough memory or if it failed to pop a string (e.g. numeric argument).
- Lines 19-35 validate the command c.
For this example all that has been implemented from CSparse are the
cs_lusol,
cs_qrsol, and
cs_cholsol solvers. If the
command is unknown, then exit with an error.
- Lines 27-30 truncate the
option in the event it was very long to avoid crashing at line 31 (important)
when creating the error string.
37 if(lusol || qrsol || cholsol) {
38 int order;
39 double tol = 1e-14;
40
41 order = sat_pop_zint_llong();
42
43 if(order < 0 || order > 3) {
44 char error[40];
45 sprintf(error,"Unknown order: %d",order);
46 sat_stack_push_string(error);
47 sat_push_real(1);
48 return(0);
49 }
50
51 t = sat_stack_pop_string_alloc();
52 if(t == NULL) {
53 sat_stack_push_string("b is not a Vector or Out of Memory.");
54 sat_push_real(1);
55 return(0);
56 }
57
58 s = sat_stack_pop_string_alloc();
59 if(t == NULL) {
60 sat_stack_push_string("A is not a Matrix Triplet List or Out of Memory.");
61 sat_push_real(1);
62 return(0);
63 }
- If a solver, then expect 3 arguments: order (int), vector (RPL array
->STR), matrix (RPL list of triplets ->STR).
- Line 41 pops the order off the
stack. This variable is used internally by CSparse. It can have an
impact on performance and memory utilization and is outside of the scope of
this document. Please refer to the CSparse book:
http://www.ec-securehost.com/SIAM/FA02.html.
- Lines 51-56 pops off the constant term vector. The constant term
vector must be an RPL array converted to a string, e.g.
"[1 2.3 .3]". If missing or too
large return an error.
- Lines 58-55 pops off the coefficient matrix. The coefficient matrix
must be an RPL list of triplets converted to a string, e.g.
"{{1 2 3.}{0 1 4.5}{2 2 .8}}".
Each triplet must be formatted {row column
value} with an array base of 0. If missing or too large return an
error.
65 sys_slowOff();
66
67 b = load_vector(t);
68 free(t);
69 A = cs_compress(load_matrix(s));
70 free(s);
71
72 if(lusol)
73 ok = cs_lusol(order, A, b, tol);
74 if(qrsol)
75 ok = cs_qrsol(order, A, b);
76 if(cholsol)
77 ok = cs_cholsol(order, A, b);
78
79 return_vector = 1;
80 }
- Line 65. Crank up the speed.
- Lines 67 and 68. Load up the constant term vector string
t in the array
b, then free up the memory used by
t. 50g RAM is scarce, if you do
not need an array or structure free it up ASAP.
- Lines 69 and 70. Load up the coefficient matrix string
s in the CSparse structure
A, then free up the memory used by
s.
- Lines 72-77. Solve it! A·x
= b. The CSparse solvers destroys b with the contents
of x. I.e. b is now the resulting column vector. The
CSparse solvers return a 1 if successful. The most common cause for
failure is lack of memory.
82 if(ok == 1 && return_vector) {
83 int i;
84 char num[21];
85 char *out;
86 int n;
87
88 n = A->n;
89 cs_free(A);
90
91 out = malloc((22*n + 4)*sizeof(char));
92 out[0] = '\0';
93
94 strcat(out,"[ ");
95 for(i=0;i < n;i++) {
96 sprintf(num,"%0.12E ",b[i]);
97 strcat(out,num);
98 }
99 strcat(out,"]");
100
101 sat_stack_push_string(out);
102 sat_push_real(0);
103 }
- Lines 88 and 89 get the length of b and free up A.
- Lines 91 and 92 create a large empty string (out)
based on the size of b.
- Lines 94-99 populate out with the
contents of b formatted as an RPL array of reals converted to a string.
- Lines 101 and 102 push the results and a "no error" status to the stack to
be processed by the wrapper.
104 else {
105 if(cholsol)
106 sat_stack_push_string("Matrix is not Positive Definite or Out of Memory.");
107 else
108 sat_stack_push_string("Bogus Inputs or Out of Memory.");
109 sat_push_real(1);
110 }
111
112 free(b);
113
114 sys_slowOn();
115
116 return(0);
117 }
- Lines 104-110 report an error to the stack if
OK != 1.
- Line 114. Back to normal speed.
- Line 116. Exit.
119 double *load_vector(char *s) {
120 int i=0;
121 double x;
122 double *b = NULL;
123
124 int k=0;
125 char c[100];
126
127 s++;
128 while(*s++ != '\0') {
129 if(*s == ' ') {
130 c[k] = '\0';
131 if(c > 0) {
132 if(sscanf(c,"%lg",&x) == 1) {
133 b = realloc(b,(i+1)*sizeof(double));
134 b[i++] = x;
135 }
136 }
137 k=0;
138 }
139 c[k++] = *s;
140 }
141
142 return(b);
143 }
- This function converts an RPL string formatted array into a C array.
- This function is pure C code, nothing HPGCC or CSparse specific here
unless you consider working around HPGCC
sscanf bugs HPGCC specific. Here is my original GCC code that
fails to function correctly with HPGCC:
double *load_vector(char *s) {
int i=0;
double x;
double *b = NULL;
while(*s++ != '\0')
if(*s == ' ')
if(sscanf(s,"%lg",&x) == 1) {
b = realloc(b,(i+1)*sizeof(double));
b[i++] = x;
}
return(b);
}
- HPGCC scanf should probably be avoided.
145 cs *load_matrix(char *s) {
146 int i,j;
147 double x;
148 cs *T;
149
150 int k=0;
151 char c[100];
152
153 T = cs_spalloc(0,0,1,1,1);
154
155 while(*s++ != '\0') {
156 if(*s == '{') {
157 s++;
158 k=0;
159 continue;
160 }
161 if(*s == '}') {
162 c[--k] = '\0';
163 if(k > 0) {
164 sscanf(c,"%d %d %lg",&i,&j,&x);
165 if(!cs_entry(T, i, j, x))
166 return(cs_spfree(T));
167 }
168 s+=3;
169 k=0;
170 continue;
171 }
172 c[k++] = *s;
173 }
174
175 return(T);
176 }
- This function converts an RPL string formatted list of triplets into a
CSparse structure..
- This function is pure C code, nothing HPGCC specific here unless you
consider working around HPGCC sscanf
bugs HPGCC specific. Here is my original GCC code that fails to function
correctly with HPGCC:
cs *load_matrix(char *s) {
int i,j;
double x;
cs *T;
T = cs_spalloc(0,0,1,1,1);
while(*s++ != '\0')
if(*s == '{')
if(sscanf(s,"{ %d %d %lg }",&i,&j,&x) == 3)
if(!cs_entry(T, i, j, x))
return(cs_spfree(T));
return(T);
}
- HPGCC scanf should probably be avoided.
Makefile
The Makefile for csparse is the same used in Part 1 with the following changes
in bold. Note the large stack requirements (-s30000).
This may need to be adjusted to support larger inputs and outputs. The
value below supports 30000 bytes.
export C_FLAGS= -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I CSparse/Include -I CSparse/Lib/stubs \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD= arm-elf-ld
export LD_FLAGS= -L$(LIBS_PATH) -LCSparse/Lib \
-T VCld.script $(LIBS_PATH)/crt0.o
export LIBS= -lcsparse -lhpg -lhplib -lgcc
...
%.hp: %.exe
$(ELF2HP) -s30000 $< $@
To build it type:
cd ~/hpgcc/sparse
make clean
make csparse.hp
Wrappers
The csparse.hp solver front-end
requires four arguments. Stack levels:
- Command. The only CSparse functions implemented in this example are
LUSOL (LU factorization),
QRSOL (QR factorization), and
CHOLSOL (Cholesky factorization).
The command must be in uppercase.
- Order. This variable is used internally by CSparse. It can have an
impact on performance and memory utilization and is outside of the scope of
this document. Please refer to the CSparse book:
http://www.ec-securehost.com/SIAM/FA02.html. For now use an order of
1 for LUSOL and
CHOLSOL and an order of 3 for
QRSOL.
- Constant term vector. This must be an RPL array (including zeros!)
converted to a string. E.g. for the original 3 panes problem the
constant term vector would be: "[-.7 0 0 0 0]".
- Coefficient matrix. This must be an RPL list of triplets (excluding
zeros!) converts to a string. E.g. for the original 3 panes problem the
coefficient matrix would be: "{{0 0 -1.}{1 1 -1.}{2 2 -1.}{3 3 -1.}{4 4 -1.}{0 3 .2}{3 0 .2}{1 4 .2}{4 1 .2}{1 0 .7}{2 1 .7}{3 4 .7}}".
Each triplet must be formatted {row(int) column(int)
value(real)} with an array base of 0.
The differences in the wrappers are in bold.
LUSOL:
|
QRSOL: |
CHOSOL: |
%%HP: T(3)A(R)F(.);
\<<
\->STR SWAP \->STR SWAP
1 "LUSOL"
:3: "EXTEND/CSPARSE" EVAL
IF
THEN
DOERR
END
OBJ\->
\>>
|
%%HP: T(3)A(R)F(.);
\<<
\->STR SWAP \->STR SWAP
3 "QRSOL"
:3: "EXTEND/CSPARSE" EVAL
IF
THEN
DOERR
END
OBJ\->
\>>
|
%%HP: T(3)A(R)F(.);
\<<
\->STR SWAP \->STR SWAP
1 "CHOLSOL"
:3: "EXTEND/CSPARSE" EVAL
IF
THEN
DOERR
END
OBJ\->
\>>
|
Each wrapper converts the constant term vector (assumed to be an RPL array) and
the coefficient matrix (assume to be an RPL list of triplets) to strings.
This conversion does add a bit of overhead. E.g. the N panes
problem with N=300 takes 7.58 seconds
to convert the constant term vector and coefficient matrix to strings. It
takes less time to actually solve the problem and push it back to the stack
(6.24 seconds). It took a total of 13.82 seconds for this wrapper and
CSparse to solve a 599x599 sparse linear system. Boo hoo! 13.82
seconds not fast enough? It is possible to remove some of the overhead and
read the constant term vector and the coefficient matrix directly from C using
HPStack and HPParser, but not without some limitations (to be discussed later in
this example). 13.82 seconds is nothing to cry about, the 50g internal
solver would have required over 5.7MB of RAM just to get started. The
closest I got with the 50g was N=50
(99x99 sparse linear system). That solution took 59.42 seconds.Absent
from all three wrappers is a lot of checking. Because of the length of the
inputs, the checking just added to the overhead. Sometimes a small wrapper
with proper documentation or a form is sufficient. There is also enough
checking in the C code to least return a Bogus Inputs error.
N Panes Problem
Now that you have a sparse linear solver, its time revisit the N panes
problem.
Like DPANES (above),
SPANES (below) will create a sparse
linear system to solve the N panes problem for any
T, R,
and N.
Sparse Panes (SPANES):
%%HP: T(3)A(R)F(.);
\<<
0 \-> t r n m @ Get T, R, and N from stack
\<<
n 2 * 1 - 'm' STO @ Compute M (matrix size)
0 m 1 - FOR i @ Create -1 diagonal coefficient matrix
i R\->I DUP -1. 3 \->LIST
NEXT
n m 1 - FOR i @ Add R elements to diagonal coefficient matrix
i n - R\->I i R\->I r I\->R 3 \->LIST
i R\->I i n - R\->I r I\->R 3 \->LIST
NEXT
0 n 2 - FOR i @ Add T elements to diagonal coefficient matrix
i 1 + R\->I i R\->I t I\->R 3 \->LIST
NEXT
n m 2 - FOR i
i R\->I i 1 + R\->I t I\->R 3 \->LIST
NEXT
n 1 - 6 * \->LIST @ Create constant term vector
t NEG 0 m 1 - NDUPN 1 + \->ARRY
\>>
\>>
The output for the original 3 pane problem would look like
this:
2: {{0 0 -1.}{1 1 -1.}{2 2 -1.}{3 3 -1.}{4 4 -1.}{0 3 .2}{3 0 .2}{1 4 .2}{4 1 .2}{1 0 .7}{2 1 .7}{3 4 .7}}
1: [-.7 0 0 0 0]
To solve using the sparse linear solver run
LUSOL then
n GET for the answer, e.g.:
Sparse Panes Solver (SPS):
%%HP: T(3)A(R)F(.);
\<<
\-> t r n @ Get T, R, and N from stack
\<<
t r n
\<< SPANES \>> TIMER @ Generate constant term vector and
2 RND "SETUP" \->TAG @ coefficient matrix, time it, tag it
UNROT
\<< LUSOL n GET \>> TIMER @ Solve it, get answer
2 RND "SOLVE" \->TAG @ Time it, tag it
SWAP
\>>
\>>
Timer code (TIMER):
%%HP: T(3)A(R)F(.);
\<<
TICKS \-> t
\<<
EVAL TICKS t - B\->R 8192 /
\>>
\>>
SPS can be used to
solve this problem for any T,
R and N.
N Panes Application
As stated above a form can sometimes take the place of a
robust wrapper.
NPANES:
%%HP: T(3)A(R)F(.);
\<<
"N Panes"
{
{ "Pass Through:" "" 0 }
{ "Reflect Back:" "" 0 }
{ "Number of Panes:" "" 0 }
}
{ }
{ 0 0 0 }
{ 0 0 0 }
INFORM
IF
THEN
OBJ\->
DROP
\<<
\-> t r n
\<<
t r n SPANES LUSOL n GET
\>>
\>>
EVAL
END
\>>Just input your values.
Then press OK.

Answer on the stack.
Dense vs. Sparse
The following table was constructed with output from
DPANES/DPS and
SPANES/SPS (winners in
bold):
| N |
Non
Zeros |
Zeros |
DPS(.7,.2,N)
|
DPS
Coeff.
Bytes(MTX)
|
DPS
Setup |
DPS
Solve |
SPS(.7,.2,N)
|
SPS
Coeff.
Bytes(STR)
|
SPS
Setup |
SPS
Solve |
| 3 |
12 |
13 |
38.0266075388% |
400 |
0.38 |
0.17 |
38.0266075388% |
140 |
0.28 |
0.34 |
| 4 |
18 |
31 |
28.6686567164% |
784 |
0.45 |
0.33 |
28.6686567164% |
208 |
0.37 |
0.39 |
| 10 |
54 |
307 |
5.6721177756% |
5776 |
1.31 |
1.91 |
5.6721177756% |
668 |
0.88 |
0.65 |
| 20 |
114 |
1407 |
.3945314511% |
24336 |
3.96 |
7.98 |
.3945314511% |
1465 |
1.75 |
1.12 |
| 30 |
174 |
3307 |
.0274666640% |
55696 |
8.24 |
20.10 |
.0274666640% |
2265 |
2.63 |
1.56 |
| 40 |
234 |
6007 |
.0019121946% |
99856 |
15.95 |
36.60 |
.0019121946% |
3056 |
3.52 |
2.03 |
| 50 |
294 |
9507 |
.0001331246% |
156816 |
30.67 |
59.42 |
.0001331246% |
3865 |
4.41 |
2.48 |
| 100 |
594 |
39007 |
|
633616 |
|
|
2.17715384293E-10% |
8457 |
8.95 |
4.79 |
| 200 |
1194 |
158007 |
|
2547216 |
|
|
5.82305444923E-22% |
17654 |
18.63 |
9.57 |
| 300 |
1794 |
357007 |
|
5740816 |
|
|
1.55744451540E-33% |
26854 |
30.25 |
13.82 |
Observations:
-
The accuracy of both methods are identical. No
disqualifications today.
-
The dense solver quickly loses any performance advantage as
the size of the matrix increases.
-
The dense setup program never had a chance. Too many
matrix copy operations.
-
There is not enough RAM for the dense solver to attempt
problems much larger than 50 (99x99 matrix).
-
The SPS total time could be significantly reduced if SPS
was an application specific C program instead of an RPL front-end to a general
purpose sparse linear solver.
-
Your 50g needs a sparse linear solver.
HPStack and HPParser
"HPStack is a package that provides easy access to the RPL stack from a C
application produced with HP-GCC" --
http://phsalmon.club.fr/phsalmon/hpstack/hpstack.html
HPStack/HPParser solves the problem of popping and pushing
lists, arrays, and other complex RPL objects from C. This handy addition
to HPGCC can make code cleaner (less buggy).
~/hpgcc/sparse/csparse2.c
is identical to ~/hpgcc/sparse/csparse.c
except that HPStack/HPParser is used to pop and push lists and arrays from and
to the stack. I will only comment on the HPStack/HPParser specific parts
of the code.
3 #include <hpstack.h>
14 list_t *t = NULL;
15 array_t *v = NULL;
54 if (hps_pop_array(&v) != HPS_OK) {
55 sat_stack_push_string("b is not a Vector.");
56 sat_push_real(1);
57 return(0);
58 }
59
60 if (hps_pop_list(&t) != HPS_OK) {
61 sat_stack_push_string("A is not a Matrix Triplet List.");
62 sat_push_real(1);
63 return(0);
64 }
65
66 sys_slowOff();
67
68 b = load_vector(v);
69 hps_array_destroy(&v);
70 A = cs_compress(load_matrix(t));
71 hps_list_destroy(&t);
-
Lines 54-58: Pop constant term vector (array) off the
stack, and point v to it, else error
out.
-
Lines 60-64: Pop coefficient matrix (list) off the
stack, and point t to it, else error
out.
-
Lines 69 and 71. Free up memory used by HPStack after
loading up A and b. NOTE: I am not sure this is
actually working, a lot of memory is in use.
84 #ifdef USE_HPSTACK_OUT
85 array_t *x = NULL;
86 int n;
87
88 n = A->n;
89 cs_free(A);
90
91 hps_array_build(&x,b,SAT_DOREAL,1,n);
92 hps_push_array(x);
93 sat_push_real(0);
94 #else
-
If -DUSE_HPSTACK_OUT
is set as a CFLAG in the Makefile, then
use HPStack functions to to create and push the resulting column vector.
Otherwise, build the array as a large string like
csparse.c.
WARNING: hps_array_build()
does not preserve the exponent. E.g.
1.33124580457E-6 is returned as
0.0000013312. Same answer, but with lost of precision. Very
small numbers (e.g. 2.17715384293E-12)
are returned as 0. That may be a problem. You will have to decide
what level of precision your application requires. Since this an example
of a general purpose sparse linear solver, care should be taking to ensure the
highest levels of accuracy and precision. The default in the Makefile is
to not enable USE_HPSTACK_OUT.
132 double *load_vector(array_t *v) {
133 int index=1;
134 double x;
135 double *b = NULL;
136
137 while(hps_list_get_real(v ,index ,&x) == HPS_OK) {
138 b = realloc(b,index*sizeof(double));
139 b[index-1] = x;
140 index++;
141 }
142
143 return(b);
144 }
146 cs *load_matrix(list_t *t) {
147 list_t *e;
148 int index=1;
149 cs *T;
150
151 T = cs_spalloc(0,0,1,1,1);
152
153 while(hps_list_get_list(t ,index++ ,&e) == HPS_OK) {
154 LONGLONG i,j;
155 double x;
156
157 hps_list_get_int(e, 1, &i);
158 hps_list_get_int(e, 2, &j);
159 hps_list_get_real(e, 3, &x);
160
161 if(!cs_entry(T, i, j, x)) {
162 return(cs_spfree(T));
163 }
164 }
165
166 return(T);
167 }
-
Lines 137-141 loop thought the array to load up b
with reals.
-
Lines 153-164 loop thought the list of lists. Each
triplet is then split up into row (int), column (int), and value (real) and
loaded in to A.
-
The load_vector
and load_matrix functions are much
cleaner thanks to HPStack.
Installing
HPStack/HPParser
Before you can compile
csparse2.c HPStack and HPParser must be downloaded and installed:
$ cd ~/hpgcc/sparse
$ wget
http://phsalmon.club.fr/phsalmon/hpstack/hpstack.zip
$ mkdir hpstack
$ cd hpstack
$ unzip ../hpstack.zip
$ cd ~/hpgcc/sparse
$ wget
http://phsalmon.club.fr/phsalmon/hpparser/hpparser.zip
$ mkdir hpparser
$ cd hpparser
$ unzip ../hparser.zip
The ~/hpgcc/sparse/Makefile
will need to be updated with the following changes
in bold.
export C_FLAGS= -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I CSparse/Include -I CSparse/Lib/stubs -I hpstack -I hpparser \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD= arm-elf-ld
export LD_FLAGS= -L$(LIBS_PATH) -LCSparse/Lib -Lhpstack -Lhpparser \
-T VCld.script $(LIBS_PATH)/crt0.o
export LIBS= -lcsparse -lstack -lparser -lhpg -lhplib -lgcc
To build it type:
cd ~/hpgcc/sparse
make clean
make csparse2.hp
csparse2.hp Wrappers
csparse.hp
LUSOL:
|
csparse2.hp LUSOL2: |
csparse2.hp LUSOL3 (-DUSE_HPSTACK_OUT): |
%%HP: T(3)A(R)F(.);
\<<
\->STR SWAP \->STR SWAP
1 "LUSOL"
:3: "EXTEND/CSPARSE" EVAL
IF
THEN
DOERR
END
OBJ\->
\>>
|
%%HP: T(3)A(R)F(.);
\<<
1 "LUSOL"
:3: "EXTEND/CSPARSE2" EVAL
IF
THEN
DOERR
END
OBJ\->
\>>
|
%%HP: T(3)A(R)F(.);
\<<
1 "LUSOL"
:3: "EXTEND/CSPARSE2" EVAL
IF
THEN
DOERR
END
\>>
|
The only differences between
LUSOL and
LUSOL2 is the change from
EXTEND/CSPARSE to
EXTEND/CSPARSE2 and omitting the
conversion to strings since HPStack functions can read directly from the stack
arrays and lists. LUSOL2 and
LUSOL3 only differ at the end, there is
no need to convert a string to an object if -DUSE_HPSTACK_OUT
was used to compile csparse2.hp.
HPStack Issues
HPStack/HPParser are great additions to HPGCC. Code
is cleaner and data better relates to data on the stack. However there are
a number of issues to be aware of.
-
Lost of precision. Exponents are dropped. This
can be an issue with very large or very small numbers.
-
Large memory requirement. I am still stumped by this
one. I instrumented csparse.c and
cspares2.c to report memory usage and
cspares2.c was consistently 2x larger
than cspares2.c. On my 50g the
largest N panes problem csparse2.hp
could handle was N=150, whereas
csparse.hp could handle
N=300.
-
Slow to parse. The speed gained by directly accessing
lists and arrays from the stack is lost by the overhead of parsing a more
complex data type. In an N panes shootout between
csparse2.hp and
csparse.hp with
N=150,
csparse2.hp bested
csparse.hp by
only 0.38 seconds. The time taken to convert the arguments to strings was
3.85 seconds. The estimated time
csparse2.hp took to pop and parse the arguments was 3.47
seconds.
Summary
Sparse matrices are used in many different engineering
applications. By utilizing CSparse and a bit of work hopefully you can
build some of those applications for your 50g.
P.S. Don't forget to get the book Direct Methods for
Sparse Linear Systems by Timothy A. Davis. This book is the
CSparse documentation.
Example: π Shootout
What is the fastest way to accurately compute the first
5000 digits of
π on the 50g? The purpose of this example is answer this question
by testing 6 different algorithms and 3 different math libraries.
All of the algorithms in this example with one exception
can be obtained from the book π Unleashed by Jörg Arndt and Christoph
Haenel. IMHO, a must read.
Before starting the hunt for the ultimate 50g π
program, you need to establish a method for measuring performance and accuracy.
Measuring Performance
Measuring performance is easy. Just instrument the
code. In the event that it is not your code, use the
TIMER code from the Sparse Linear
Solver example.
Timer code (TIMER):
%%HP: T(3)A(R)F(.);
\<<
TICKS \-> t
\<<
EVAL TICKS t - B\->R 8192 /
\>>
\>>
Simply place what you want timed on the stack including
stack arguments then run TIMER, e.g.:
<< 352 PICHUD >>
TIMER
The results of PICHUD will be returned to
the stack with the time in seconds it took to execute as the first stack item.
Checking Accuracy
This following C program (ckpi.c)
takes a single filename as an argument and compares it digit for digit to the
file pi1m.txt.
ckpi returns the total number of
digits and the number or correct π digits.
All C file I/O is directed to the SD card not the 50g
HOME file system. The file
~/hpgcc/pies/pi1m.txt must be copied
from your workstation to the root of your SD card.
1 #include <hpgcc49.h>
2
3 char getnextdigit(FILE *fp);
4
5 int main(void)
6 {
7 FILE *fp1, *fp2;
8 signed char c1, c2;
9 char *file1, *file2 = "pi1m.txt";
10 char errormsg[30], fname[13];
11 int num=0, tnum;
12 SAT_STACK_ELEMENT e;
13 SAT_STACK_DATA d;
14
15 sat_get_stack_element(1,&e);
16 sat_decode_stack_element(&d,&e);
17
18 if (d.type == SAT_DATA_TYPE_STRING) {
19 file1 = str_unquote(d.sval,'\'');
20 }
21 else {
22 sat_stack_push_string("Missing Filename");
23 sat_push_real(1);
24 return(0);
25 }
- Lines 12-16 points to (not pops) the first stack element.
- Lines 18-25 check that the first stack element is a string, if not return
an error. If an error the stack is left unchanged--useful for correcting
typos. In the event that a string contains single quotes line 19 will
remove them. This is useful for wrappers that use
->STR when a user passes a filename
surrounded by single quotes.
27 if((fp1 = fopen(file1,"r")) == NULL) {
28 strncpy(fname,file1,12);
29 fname[12] = '\0';
30 sprintf(errormsg,"Cannot read: %s",fname);
31
32 sat_stack_push_string(errormsg);
33 sat_push_real(1);
34 return(0);
35 }
36
37 if((fp2 = fopen(file2,"r")) == NULL) {
38 strncpy(fname,file2,12);
39 fname[12] = '\0';
40 sprintf(errormsg,"Cannot read: %s",fname);
41
42 sat_stack_push_string(errormsg);
43 sat_push_real(1);
44 return(0);
45 }
- Lines 27-45 verify that both files (user submitted and hard coded
pi1m.txt) can be read. If
not, return error. Stack is left unchanged.
47 sat_stack_drop();
48 sys_slowOff();
49
50 while((c1 = getnextdigit(fp1)) != EOF && (c2 = getnextdigit(fp2)) != EOF)
51 if(c1 == c2)
52 num++;
53 else
54 break;
- Line 47: Drop filename from stack.
- Line 48: Crank up the speed.
- Linues 50-54: Digit to digit check.
56 tnum = num;
57 if(c1 != EOF)
58 tnum++;
59 while((c1 = getnextdigit(fp1)) != EOF)
60 tnum++;
- Continue to count remaining digits for digit total.
62 fclose(fp1);
63 fclose(fp2);
64
65 sat_push_zint_llong(tnum);
66 sat_push_zint_llong(num);
67 sat_push_real(0);
68
69 sys_slowOn();
70 return(0);
71 }
- Lines 65 and 66 push the total number of digits and the number of correct
digits to the stack as integers.
- Line 67 pushes a 0 return code to the wrapper signaling "OK, no problems".
73 char getnextdigit(FILE *fp) {
74 signed char c;
75
76 while((c = fgetc(fp)) != EOF)
77 if(isdigit(c))
78 return(c);
79
80 return(EOF);
81 }
-
Different π programs have different formatting (decimal
point, spaces, new lines, etc...). This function will get the next digit
in the file and return.
Check π Wrapper
%%HP: T(3)A(R)F(.);
\<<
\->STR
:3: "EXTEND/CKPI" EVAL
IF
THEN
DOERR
END
"Correct Dgts" \->TAG SWAP
"Total Digits" \->TAG SWAP
\>>
-
Convert the first stack argument to a string, just in case
'FILENAME' was entered instead of "FILENAME". Lines 18-25 in
ckpi will strip off single quotes.
-
Run CKPI, check
for 0 or 1 return code, error on non-zero.
-
Tag the results.
This wrapper could be more robust (e.g. not calling
->STR when the stack is empty).
An exercise left for the reader.
Makefile
The Makefile for all the code in this example is the same used in Part 1 with the following changes
in bold. The changes should look familiar if you read the first
two examples. IANS, add support for libraries and increase the bytes
allocated for stack interaction.
export C_FLAGS = -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I libtommath-0.41 -I libtommath-0.41/stubs \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD = arm-elf-ld
export LD_FLAGS = -L$(LIBS_PATH) -L libtommath-0.41 -T VCld.script $(LIBS_PATH)/crt0.o
export LIBS = -ltommath -ldecnumber -lhpg -lhplib -lgcc
...
%.hp: %.exe
$(ELF2HP) -s6000 $< $@
...
%_local: %.c
gcc -Wall -g -o $@ $< -DHPGCC -I $(HPAPINE)/include/ \
-DHPAPINE -L $(HPAPINE)/lib/ -lhpapine \
-I libtommath-0.41 -L libtommath-0.41 -ltommath_local \
$(shell pkg-config --libs gdk-2.0 gthread-2.0)
To compile: make program.hp or
make program_local (for HPAPINE).
Chudnovsky
The Chudnovsky
brothers discovered this Ramanujan-type series and used it multiple times to take the title
for the most π digits calculated. The last time was in 1996 with 8
billion digits.
What a beast! Fortunately, no work is required to
implement this algorithm for the 50g because it is already
included as part of HPGCC. To maintain consistency with the rest of this
document copy and rename the HPGCC included
chud_pi.c as pichud.c:
$ cd ~/hpgcc/pies
$
cp ~/hpgcc/2.0SP2/examples/decnumber/Chudnovsky/chud_pi.c pichud.c
$
indent -kr -ts4 pichud.c
$
rm pichud.c~
pichud.c uses IBM's decNumber (http://www2.hursley.ibm.com/decimal/decnumber.html)
as an arbitrary-precision library. This frees up the developer from the
need
to create application specific arbitrary-precision code. decNumber will be
discussed in more detail in the next π example (Gauss AGM).
I will withhold any comments on this code since there is
nothing HPGCC specific in pichud.c that
has not been discussed before (with the exception of decNumber (to be discussed
later)).
pichud takes one
real argument: number of iterations. Each iteration of this algorithm produces 14 to 15 π
digits. After a few trials I determined that at least 352
iterations is required to produce at least 5000 correct π digits. Unlike
the rest of the π code in this article,
pichud does not output to a file, but returns a very large string to
the stack instead. That will be a problem for
ckpi since it expects an input file
for π verification. Instead of adding string support to
ckpi or file support to
pichud I created a string to file
utility. I felt that this utility would have use elsewhere.
String to File
s2fl takes two
stack arguments. Both must be strings. Stack level two contains the
string to be save into the file specified at stack level one.
1 #include <hpgcc49.h>
2
3 int main(void)
4 {
5 char *filename, *s;
6 SAT_STACK_ELEMENT e;
7 SAT_STACK_DATA d;
8 FILE *fp;
9
10 sat_get_stack_element(1, &e);
11 sat_decode_stack_element(&d, &e);
12 if (d.type == SAT_DATA_TYPE_STRING) {
13 filename = str_unquote(d.sval, '\'');
14 } else {
15 sat_stack_push_string("Missing Filename");
16 sat_push_real(1);
17 return (0);
18 }
- Lines 10-11 points to (not pops) the first stack element.
- Lines 12-18 check that the first stack element is a string, if not return
an error. If an error the stack is left unchanged--useful for correcting
typos. In the event that a string contains single quotes, then line 13 will
remove them. This is useful for wrappers that use
->STR when a user passes a filename
surrounded by single quotes.
20 sat_get_stack_element(2, &e);
21 sat_decode_stack_element(&d, &e);
22 if (d.type == SAT_DATA_TYPE_STRING) {
23 sat_stack_drop();
24 s = sat_stack_pop_string_alloc();
25 } else {
26 sat_stack_push_string("Missing String");
27 sat_push_real(1);
28 return (0);
29 }
- Lines 20-21 points to (non pops) the 2nd stack element. Stack
element one (filename) is still present.
- Lines 22-29 check that the 2nd stack element is a string, if not return an
error. If an error the stack is left unchanged. Both the string
and the filename are still present. It would be a shame to lose a string that took a long
time to generate because of a typo.
- Lines 22-23: If a string, then pop off and discard filename (already
verified and saved above).
- Line 24: Allocate memory for string, pop off stack, point
s to it.
sat_stack_pop_string_alloc() must be
used in this case vs. str_unquote()
above because str_unquote() only
returns a maximum of 511 bytes. Ok for filenames, but not for long π
strings.
31 if ((fp = fopen(filename, "w")) == NULL) {
32 char errormsg[30];
33 char fname[13];
34
35 strncpy(fname, filename, 12);
36 fname[12] = '\0';
37 sprintf(errormsg, "Cannot open: %s", fname);
38
39 sat_stack_push_string(errormsg);
40 sat_push_real(1);
41 return (0);
42 }
- Lines 31-42 open the filename, on error push error message to stack with a
return code of 1 to be processed by the wrapper.
- Lines 35-37 create the error message with a truncated filename in the
event that the filename is too long. This is important to prevent a
crash at line 37.
44 fprintf(fp, "%s", s);
45 fclose(fp);
46
47 sat_push_real(0);
48 return (0);
49 }
You may be asking yourself, "why not just save the string
to port 3 from RPL?" You can, but all RPL objects saved to port 3 (SD
card) contain a header that will interfere with
ckpi. You can test this with Cygwin/Linux utility hexdump
-C.
<< "ABC" "FILENAME" S2FL
>> EVAL:
00000000 41 42 43 |ABC|
<< "ABC" 3:FILENAME STO
>> EVAL:
00000000 48 50 48 50 34 39 2d 58 2c 2a f0 00 00 41 42 43 |HPHP49-X,*...ABC|
I suppose it would be possible to write all HPGCC
programs to check and ignore this header. But, if the data must be shared
via SD shuttle transfers to your workstation, it would be inconvenient to have
to change all programs that work with text files to ignore this header.
You may have also asked yourself, "what about
fl2s?"
It's unnecessary. RPL RCL will recall to the stack strings from files with
or without the 50g header. IOW, FL2S:
<< 3 ->TAG RCL >>
String to File Wrapper
%%HP: T(3)A(R)F(.);
\<<
\->STR
:3: "EXTEND/S2FL" EVAL
IF
THEN
DOERR
END
\>>
This wrapper could be more robust (e.g. not calling
->STR when the stack is empty).
Another exercise left for the reader.
Chudnovsky Wrapper
%%HP: T(3)A(R)F(.);
\<<
\->NUM
:3: "EXTEND/PICHUD" EVAL
"PICHUD.TXT" S\->FL
\>>
pichud requires a
single real argument for the number of iterations,
->NUM will convert most stack arguments
to a real. pichud returns no
error messages or return codes to the stack, so there is no need for error
checking code. pichud will return π as a string of digits. The last
statement will save the results of pichud
as the file PICHUD.TXT.
Run It/Check It
To get a timing and at least 5000 correct digits run:
<< 352 PICHUD >> TIMER
The screen will clear and print a single "." per iteration.
When complete you will be returned to the RPL stack with a
single number representing the number of seconds
pichud took to run:
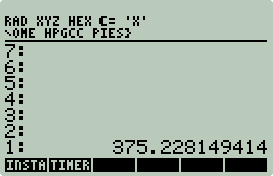
The output should be on the SD card as
PICHUD.TXT. To verify the number
of correct digits use ckpi. E.g.:
<< "PICHUD.TXT" CKPI >>
EVAL
Output:

pichud computed a
total of 5555 digits in 375 seconds. 5006 were correct π digits.
Gauss AGM
From 1996 to 2002 AGM-type algorithms have dominated as the
the algorithm of champions.
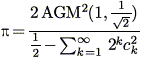
An attractive feature of this algorithm is that it
converges very quickly. Each iteration doubles the number of π digits
while the time per iteration remains constant. Impressive. Only 14
iterations are needed for 5000 digits. However, each iteration of this
algorithm must be performed using a level of numeric precision that is at least
as high as that desired for the final result [7]. This is not the case
for the Chudnovsky program above. Past 5000 digits
chud_pi will dynamically increase the
precision. Nice.
The specific Gauss AGM implementation below (piagm.c) is the Schönhage
variant. And like the Chudnovsky implementation above it also uses IBM's decNumber
as an arbitrary-precision library. NOTE: This example is not a substitute
for the decNumber documentation, please read:
http://www2.hursley.ibm.com/decimal/decnumber.pdf.
piagm.c:
1 #define DECNUMDIGITS 5010
2 #include <decNumber.h>
3 #include <hpgcc49.h>
4 #include <hpgraphics.h>
5
6 #ifndef HPAPINE
7 extern unsigned int __heap_ptr,_heap_base_addr;
8 int freemem();
9 #endif
10
11 int decNumberIsPrec(decNumber, decNumber, decNumber, decContext);
12 int decNumberIsLess(decNumber, decNumber, decContext);
- Line 1: DECNUMDIGITS is the
decNumber precision. I.e., each decNumber will have up to 5010 digits.
A handful of digits past 5000 is required to accurately compute the first 5000
π digits.
- Line 2: The decNumber header.
- Line 3: Graphics? This is needed to turn on the indicators.
More on this later.
- Lines 6-9: If not using HPAPINE add support for memory usage
reporting.
More on this later.
14 int main(void) {
15 decNumber a, b, A, B, s, k, x, y, t;
16 decNumber temp1, temp2, temp3, one, two, four, ten, prec;
17 decNumber z;
18 decContext set;
19 FILE *fp;
20 char out[DECNUMDIGITS+1];
21 int zz, kk=0;
22 int start, end;
23 #ifndef HPAPINE
24 int mem;
25
26 mem = freemem();
27 #endif
- Lines 15-18 define decNumber variables.
- Lines 20: Create a string variable to output the result.
- Lines 23-27: If not using HPAPINE, then store in
mem the amount of free memory.
29 if((fp = fopen("piagm.log","w")) == NULL) {
30 char errormsg[30];
31
32 sprintf(errormsg,"Cannot open: %s","piagm.log");
33
34 sat_stack_push_string(errormsg);
35 sat_push_real(1);
36 return(0);
37 }
38
39 sys_slowOff();
40 clear_screen();
- pigam creates two output files:
- Lines 29-37: Return error if failed to
open piagm.log
for writing.
- Lines 39-40: Up the speed and clear the
screen. It should be obvious by now that the number of digits is hard
coded. Nothing is read from the stack.
42 printf("PI AGM - Hold down ENTER to exit\n\n");
43
44 decContextDefault(&set, DEC_INIT_BASE);
45 set.traps = 0;
46 set.digits = DECNUMDIGITS;
47
48 decNumberFromString(&a, "1", &set);
49 decNumberFromString(&A, "1", &set);
50 decNumberFromString(&B, "0.5", &set);
51 decNumberFromString(&s, "0.5", &set);
52 decNumberFromString(&k, "0", &set);
53 decNumberFromString(&x, "0", &set);
54 decNumberFromString(&y, "1", &set);
55
56 decNumberFromString(&one, "1", &set);
57 decNumberFromString(&two, "2", &set);
58 decNumberFromString(&four, "4", &set);
59 decNumberFromString(&ten, "10", &set);
60
61 decNumberFromString(&prec, "1E-5000", &set);
- Line 42 prints a line instructing the user on the use of the
ENTER key. At the end of each
iteration a check is performed to see if any key is being held down, if so
exit the loop. AFAIK, HPGCC keystrokes are not buffered and that is why
the message reads, "Hold down". Each iteration takes about 8 seconds.
The key does not need to be held down long to interrupt the computation.
- Lines 44-61 setup the decNumber environment and initialize the decNumber
variables.
63 start = sys_RTC_seconds();
64 while(!decNumberIsPrec(x,y,prec,set)) {
65 int start, end;
66
67 start = sys_RTC_seconds();
68
69 // k = k + 1
70 decNumberAdd(&k, &k, &one, &set);
71
72 // status iterations
73 kk++;
74 printf("Iteration: %2d ",kk);
75 fprintf(fp,"Iteration: %2d ",kk);
76 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
- Line 63: Store the current time. This is used at the end to
report the total time.
- Line 64: Check the difference between the last two iterations.
If the difference is greater than 1E-5000, then continue to iterate.
- Line 65: Define start and
end again as local loop variables to
report the timing of each loop. Not to be confused with
start and
end outside the loop. This is
probably not a good idea, it can lead to confusing code.
- Line 67: Stores the current time for this iteration.
- Line 70: Perform first decNumber arithmetic operation. This is
what arbitrary precision in C can look like.
- Lines 73-75: Print the first half of the iteration information.
The 2nd half comes at the end of the loop.
- Line 76: Turn on the hour glass indicator. In the event text
scrolls off the screen the indicator also scrolls of the screen. To get
around this problem turn on the indicator each time a line is printed.
78 // x = y
79 decNumberCopy(&x, &y);
80
81 // t = (A+B)/4.0
82 decNumberAdd(&temp1, &A, &B, &set);
83 decNumberDivide(&t, &temp1, &four, &set);
84
85 // b = sqrt(B)
86 decNumberSquareRoot(&b, &B, &set);
87
88 // a = (a+b)/2.0
89 decNumberAdd(&temp1, &a, &b, &set);
90 decNumberDivide(&a, &temp1, &two, &set);
91
92 // A = a^2.0
93 decNumberMultiply(&A, &a, &a, &set);
94
95 // B = (A-t)*2.0
96 decNumberSubtract(&temp1, &A, &t, &set);
97 decNumberMultiply(&B, &temp1, &two, &set);
98
99 // s = s + (B-A)*2^k
100 decNumberSubtract(&temp1, &B, &A, &set);
101 decNumberPower(&temp2, &two, &k, &set);
102 decNumberMultiply(&temp3, &temp1, &temp2, &set);
103 decNumberAdd(&s, &s, &temp3, &set);
104
105 // y = (a+b)^2.0/(2.0 * s)
106 decNumberAdd(&temp1, &a, &b, &set);
107 decNumberMultiply(&temp2, &temp1, &temp1, &set);
108 decNumberMultiply(&temp3, &two, &s, &set);
109 decNumberDivide(&y, &temp2, &temp3, &set);
- Lines 78-109: This is the AGM computation that takes place on each
iteration. To make it a bit more readable I added comments above each
section.
111 end = sys_RTC_seconds();
- Line 111: End of loop, get loop time.
113 // status digits
114 decNumberSubtract(&z, &y, &x, &set);
115 decNumberAbs(&z, &z, &set);
116 zz=0;
117 while(decNumberIsLess(z,one,set)) {
118 decNumberMultiply(&z, &z, &ten, &set);
119 zz++;
120 }
121 printf("Digits: %4d ",zz);
122 fprintf(fp,"Digits: %4d ",zz);
123
124 printf("Tm: %2d",end-start);
125 fprintf(fp,"Tm: %2d\n",end-start);
126
127 if(keyb_isAnyKeyPressed())
128 break;
129 }
- Lines 113-122: Count the number of correct digits and report.
This adds unnecessary overhead (just under 1 second), but I find the output
educational.
- Lines 124-125: Report the loop time.
- Lines 127-128: Check for a held key. If down, exit loop, but
not program, intermediate results will be returned.
130 end = sys_RTC_seconds();
131
132 printf("\n");
133 fprintf(fp,"\n");
134 printf(" time(s): %d\n",end-start);
135 fprintf(fp," time(s): %d\n",end-start);
136 #ifndef HPAPINE
137 printf("bytes used: %d",mem-freemem());
138 fprintf(fp,"bytes used: %d\n",mem-freemem());
139 #endif
140 fclose(fp);
- Line 130: Get final end time.
- Lines 132-135: Report time to screen and to log file.
- Lines 136-139: Report memory used to screen and to log file.
- Line 140: Close file.
142 decNumberToString(&x, out);
143 if((fp = fopen("piagm.txt","w")) == NULL) {
144 char errormsg[30];
145
146 sprintf(errormsg,"Cannot open: %s","piagm.txt");
147
148 sat_stack_push_string(errormsg);
149 sat_push_real(1);
150 return(0);
151 }
152 fprintf(fp,"%s\n",out);
153 fclose(fp);
- Line 142: Convert x (π)
to a string.
- Lines 143-153: Open
piagm.txt
for writing, error on failure. If OK, then output π string.
155 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_WHITE);
156 sat_push_real(0);
157 beep();
158 sys_slowOn();
159 WAIT_CANCEL;
160 return(0);
161 }
- Line 155: Turn off busy indicator.
- Line 156: Push 0 (OK) to stack to be processed by wrapper.
- Line 157: Beep. HPGCC programs will drain the battery if left
unchecked. This gets the users attention.
- Line 158: Slow down, save battery in the event the user did not hear
the beep.
- Line 159: Wait for user to press ON (CANCEL).
- Line 160: Exit.
163 int decNumberIsPrec(decNumber a, decNumber b, decNumber c, decContext ctx)
164 {
165 decNumber temp1, temp2;
166 decNumber cmp;
167
168 decNumberSubtract(&temp1, &a, &b, &ctx);
169 decNumberAbs(&temp2, &temp1, &ctx);
170 decNumberCompare(&cmp, &temp2, &c, &ctx);
171 return(decNumberIsNegative(&cmp));
172 }
173
174 int decNumberIsLess(decNumber a, decNumber b, decContext ctx)
175 {
176 decNumber cmp;
177
178 decNumberCompare(&cmp, &a, &b, &ctx);
179 return(decNumberIsNegative(&cmp));
180 }
- Lines 163-180: Define decNumber functions to do simple comparative
checks.
182 #ifndef HPAPINE
183 int freemem()
184 {
185 register unsigned int stack_ptr asm ("sp");
186 unsigned int base;
187
188 base=(__heap_ptr == 0)? _heap_base_addr:__heap_ptr;
189
190 return stack_ptr-base;
191 }
192 #endif
AGM Wrapper
%%HP: T(3)A(R)F(.);
\<<
:3: "EXTEND/PIAGM" EVAL
IF
THEN
DOERR
END
\>>
This is about as basic as it gets. No arguments to
process. Just process errors.
Run It/Check It
Just run it. The output should look like this:

And end like this:
Check it:
<< "PIAGM.TXT" CKPI >>
EVAL
Output:

piagm computed a
total of 5010 digits (5005 correct π digits) in 122 seconds using 31104 bytes.
Spigot Algorithm
This is probably my favorite π algorithm. Spigot (streaming)
algorithms display the digits as they are computed making this the most
entertaining algorithm. All other algorithms
must wait until the end of the computation. The spigot algorithm used in
this example is a faster variant of the original discovered by Stanley Rabinowitz and Stanley Wagon:
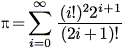
The faster variant by Jörg Arndt and Christoph Haenel (π
Unleashed) computes π base 10,000 instead of π base 10.
spigot.c takes a
single argument (number of digits) and returns to the stack 5 statistics
with tags to be processed by the wrapper.
1 #include <hpgcc49.h> //the standard HP lib
2 #include <hpgraphics.h>
3
4 #ifndef HPAPINE
5 extern unsigned int __heap_ptr,_heap_base_addr;
6 int freemem();
7 #endif
- Line 2: Include graphics headers for indicator support.
- Lines 4-7: If not using HPAPINE enable free memory query support.
9 int main(void) {
10 unsigned int *a, b, c, d = 0, e = 0, f = 10000, g, h = 0;
11 int start, end, cc = 0, ndigits;
12 FILE *fp;
13 char *filename = "spigot.txt";
14 char errormsg[40];
15 #ifndef HPAPINE
16 int mem;
17
18 mem = freemem();
19 #endif
- Line 13: Output will be saved to
spigot.txt.
- Lines 15-19: If not use HPAPINE query free memory and store it in
mem.
21 ndigits = sat_pop_real(); //get ndigits from stack
22 if(ndigits < 1) {
23 sat_push_zint_llong((int)ndigits);
24 sat_stack_push_string("PI digits must be > 0");
25 sat_push_real(1);
26 return(0);
27 }
28 if(ndigits % 4 != 0)
29 ndigits+=4;
30 c=(ndigits/4+1)*14;
- Line 21: Get number of π digits from
stack. Although an integer is required
sat_pop_real()
is used for two reasons:
- Using
->NUM
in the wrapper is very convenient and
->NUM
always converts to a real.
- HPAPINE will not pop off an integer.
I use HPAPINE for all development, it is a real time saver, so I do not mind
coding around HPAPINE issues.
- Lines 22-27: If
ndigits
is not greater than 0 then error out.
- Lines 28-29: This code rounds up to the
nearest multiple of 4 since this algorithm produces 4 digits (base 10,000) at
a time.
- Line 30: Determine how many base 10,000
digits will be required to compute the number of desired digits. Read π
Unleashed for algorithm details.
32 if((fp = fopen(filename,"w")) == NULL) {
33 sprintf(errormsg,"Cannot open: %s",filename);
34
35 sat_stack_push_string(errormsg);
36 sat_push_real(1);
37 return(0);
38 }
39
40 sys_slowOff(); //max speed
41
42 if((a=malloc(c*sizeof(*a))) == NULL) {
43 sprintf(errormsg,"Cannot allocate %d bytes\n",(int)(c*sizeof(*a)));
44 sat_stack_push_string(errormsg);
45 sys_slowOn();
46 sat_push_real(1);
47 return(0);
48 }
49
50 clear_screen(); //clear the screen
51 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
- Lines 32-38: Open spigot.txt
for output or error out.
- Line 40: Go fast.
- Line 42-48: Allocate digit space. If pointer returned as NULL
error out.
- Line 51: Turn on busy indicator.
53 start = sys_RTC_seconds(); //get start time in seconds since 1/1/1970
54 while ((b=c-=14) > 0) { //logic, compute 4 digits of pi at a time then display
55 while(--b > 0) {
56 d *= b;
57 if (h == 0)
58 d += 2000 * f;
59 else
60 d += a[b] * f;
61 g=b+b-1;
62 a[b] = d % g;
63 d /= g;
64 }
65 printf("%04d", e + d/f);
66 fprintf(fp,"%04d", e + d/f);
67 cc+=4;
68 if(cc % 32 == 0) {
69 printf("\n");
70 fprintf(fp,"\n");
71 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
72 }
73 if(keyb_isAnyKeyPressed()) //hold any key to stop, do not use ON
74 break;
75 d = e = d % f;
76 h = 4;
77 }
78 end = sys_RTC_seconds(); //get end time in seconds since 1/1/1970
- Lines 53-78: Loop and time until number of digits computed.
- Lines 68-72: If 32 digits have been printed, then print a newline
and turn on busy indicator. This needs to be done each time a newline is
printed in the event text scrolls off the screen and wipes out the indicator.
- Lines 73-74: This well behaved program will exit the loop if a key a
pressed. The program will return intermediate results.
79 if(cc % 32 != 0) {
80 printf("\n");
81 fprintf(fp,"\n");
82 }
83 printf("\n");
84 fprintf(fp,"\n");
85 fclose(fp);
- Lines 79-85: If last line is not 32 digits long, print a newline.
Close spigot.txt.
87 printf("bytes alloc: %d\n",(ndigits/4+1)*14*(int)sizeof(*a));
88 sat_push_zint_llong((ndigits/4+1)*14*(int)sizeof(*a));
89 sat_stack_push_string("bytes alloc");
90 #ifndef HPAPINE
91 printf(" bytes used: %d\n",mem-freemem());
92 sat_push_zint_llong(mem-freemem());
93 sat_stack_push_string("bytes used");
94 #endif
95 printf(" time(s): %d\n",end-start);
96 sat_push_zint_llong(end-start);
97 sat_stack_push_string("time(s)");
98
99 printf(" digits: %d\n",cc);
100 sat_push_zint_llong(cc);
101 sat_stack_push_string("digits");
102
103 if(end-start == 0) {
104 printf(" digits/s: NAN");
105 sat_stack_push_string("NAN");
106 }
107 else {
108 printf(" digits/s: %.2f",(float)cc/(float)(end-start));
109 sat_push_real(((cc*100)/(end-start) + .5)/100.0);
110 }
111 sat_stack_push_string("digits/s");
- Lines 87-111: Print stats to screen and push stats to stack with
tags. See wrapper below.
- Lines 90-94: If not using HPAPINE print out measured memory usage.
113 sat_push_real(0);
114 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_WHITE);
115 beep();
116 sys_slowOn(); //normal speed
117 WAIT_CANCEL; //loop until ON pressed
118 return(0);
119 }
- Line 113: Push a 0 (OK) to the stack.
- Line 114: Turn off busy indicator.
- Line 115: Alert user that program is waiting for input.
- Line 116: Slow down to save battery life.
- Line 117: Wait for user input. Press ON(CANCEL) to exit.
- Line 118: Exit.
121 #ifndef HPAPINE
122 int freemem()
123 {
124 register unsigned int stack_ptr asm ("sp");
125 unsigned int base;
126
127 base=(__heap_ptr == 0)? _heap_base_addr:__heap_ptr;
128
129 return stack_ptr-base;
130 }
131 #endif
Spigot Wapper
%%HP: T(3)A(R)F(.);
\<<
\->NUM
:3: "EXTEND/SPIGOT" EVAL
IF
THEN
DOERR
END
9 5 FOR i
\->TAG i ROLLD
-1 STEP
\>>
-
Convert stack argument to a real.
-
Execute spigot
from SD card.
-
If an error DOERR
and die.
-
If not an error loop through the stack and attach tags to
values.
The stack output of
spigot should look something like this:
11: 70056
10: "bytes alloc"
9: 77092
8: "bytes used"
7: 46
6: "time(s)"
5: 5000
4: "digits"
3: 108.695
2: "digits/s"
1: 0
The zero at position 1 is the return code (OK). The
<< 9 5 FOR i ->TAG i ROLLD -1 STEP >>
code does the match up. To do this with your own code, output to the stack
value, string tag pairs. Replace the
9 with
2*n-1 and the
5 with
n where
n is the number of pairs.
This wrapper could be more robust (e.g. not calling
->NUM when the stack is empty).
Yet another exercise left for the reader.
Run It/Check It
To run it put 5000
on the stack and execute the SPIGOT
wrapper. Output should look like this:
And end like this:
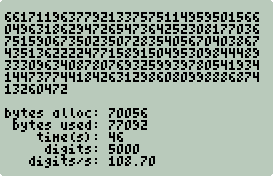
Press ON(CANCEL) to exit. The same stats reported to the screen are also
pushed to the stack as value, tag string pairs. The wrapper does
the match up.

Check it with:
<< "SPIGOT.TXT" CKPI >>
EVAL

A new record. 5000 correct digits in 46 seconds.
How high can you go? Not very high. The limited size of unsigned 32
bit integers prevents this algorithm from accurately computing more than 32373
digits. You'll run out of memory around 25000 digits, so no need to worry
about it on the 50g. The HPAPINE version however can get all 32373 digits.
Even if your 50g had 64 bit integers and lots of RAM this algorithm has a flaw
that prevents more than 54932 digits to be computed. This flaw is
addressed with the Unbounded Spigot Algorithm.
Unbounded Spigot Algorithm
An Unbounded Spigot Algorithm was created by Jeremy Gibbons
to address the limitations of the original Rabinowitz and Wagon spigot algorithm
above. You can read all about it here:
http://www.comlab.ox.ac.uk/oucl/work/jeremy.gibbons/publications/spigot.pdf.
uspi is a port of
the Haskell program that appears in the aforementioned paper by Gibbons:
> pi = g(1,0,1,1,3,3) where
> g(q,r,t,k,n,l) = if 4*q+r-t<n*t
> then n : g(10*q,10*(r-n*t),t,k,div(10*(3*q+r))t-10*n,l)
> else g(q*k,(2*q+r)*l,t*l,k+1,div(q*(7*k+2)+r*l)(t*l),l+2)
uspi like the
Haskell program requires the use of arbitrary-precision arithmetic, specifically
very large integers. And like the Haskell program it will run until out of
memory. Unlike the Haskell program, you can specify a maximum number of
digits. When this limit is reached or memory runs out the loop terminates.
How large is large? To compute 5000 π digits
using this algorithm requires integers as long as 67856 digits. That's greater than 1067855.
The number of particles in the universe is only 1080.
Large numbers also use a large amount of RAM. 28180 bytes of memory is
required to store a 67856 digit number.
I originally wrote this using decNumber. Dumb.
5000 digits took 26 minutes on my workstation. decNumber is not optimized
for large integers, but LibTomMath [8] is. After rewriting the code for
LibTomMath, I was able to produce 5000 digits in 25 seconds on my workstation.
This is a significant improvement, but 5000 digits in 25 seconds on a
workstation? It should have taken a split second. This is clearly
not an efficient way to compute π, but it is an excuse to work with very large
integers on the 50g.
LibTomMath
LibTomMath is a free open source portable number theoretic
multiple-precision integer library written entirely in C [8]. LibTomMath
is documented in the book BigNum MATH by St. Denis.
Building LibTomMath for the 50g is easy:
-
Change to working directory:
$ cd ~/hpgcc/pies
-
Download and extract
ltm-0.41.tar.bz2:
$ wget
http://libtom.org/files/ltm-0.41.tar.bz2
$ tar jxvf
ltm-0.41.tar.bz2
-
Create stubs. See the LogGamma example for an explanation
as to why this is necessary.
$ cd
libtommath-0.41
$ mkdir stubs
$
echo '#include <hpgcc49.h>' >stubs/ctype.h
$
echo '#include <hpgcc49.h>' >stubs/stdio.h
$
echo '#include <hpgcc49.h>' >stubs/stdlib.h
$
echo '#include <hpgcc49.h>' >stubs/string.h
-
Create ~/hpgcc/pies/libtommath-0.41/Makefile.hpgcc.
This is a hybrid of a standard HPGCC Makefile and the Makefile included with
LibTomMath. By examining both Makefiles you can see that most of the
differences are in the compiler and compiler flag settings.
#Makefile for HPGCC
INCLUDE_PATH= $(HPGCC)/include
LIBS_PATH= $(HPGCC)/lib
ELF2HP_PATH=elf2hp
export CUR_DIR= $(shell pwd)
export CC= arm-elf-gcc
export AR= arm-elf-ar
export RANLIB= arm-elf-ranlib
export CFLAGS= -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-I$(INCLUDE_PATH) -I stubs -L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD= arm-elf-ld
#version of library
VERSION=0.41
CFLAGS += -I . -Wall -W -Wshadow -Wsign-compare
ifndef MAKE
MAKE=make
endif
ifndef IGNORE_SPEED
#for speed
CFLAGS += -O3 -funroll-loops
#for size
#CFLAGS += -Os
#x86 optimizations [should be valid for any GCC install though]
CFLAGS += -fomit-frame-pointer
#debug
#CFLAGS += -g3
endif
#install as this user
ifndef INSTALL_GROUP
GROUP=wheel
else
GROUP=$(INSTALL_GROUP)
endif
ifndef INSTALL_USER
USER=root
else
USER=$(INSTALL_USER)
endif
default: libtommath.a
#default files to install
ifndef LIBNAME
LIBNAME=libtommath.a
endif
HEADERS=tommath.h tommath_class.h tommath_superclass.h
#LIBPATH-The directory for libtommath to be installed to.
#INCPATH-The directory to install the header files for libtommath.
#DATAPATH-The directory to install the pdf docs.
DESTDIR=
LIBPATH=/usr/lib
INCPATH=/usr/include
DATAPATH=/usr/share/doc/libtommath/pdf
OBJECTS=bncore.o bn_mp_init.o bn_mp_clear.o bn_mp_exch.o bn_mp_grow.o bn_mp_shrink.o \
bn_mp_clamp.o bn_mp_zero.o bn_mp_set.o bn_mp_set_int.o bn_mp_init_size.o bn_mp_copy.o \
bn_mp_init_copy.o bn_mp_abs.o bn_mp_neg.o bn_mp_cmp_mag.o bn_mp_cmp.o bn_mp_cmp_d.o \
bn_mp_rshd.o bn_mp_lshd.o bn_mp_mod_2d.o bn_mp_div_2d.o bn_mp_mul_2d.o bn_mp_div_2.o \
bn_mp_mul_2.o bn_s_mp_add.o bn_s_mp_sub.o bn_fast_s_mp_mul_digs.o bn_s_mp_mul_digs.o \
bn_fast_s_mp_mul_high_digs.o bn_s_mp_mul_high_digs.o bn_fast_s_mp_sqr.o bn_s_mp_sqr.o \
bn_mp_add.o bn_mp_sub.o bn_mp_karatsuba_mul.o bn_mp_mul.o bn_mp_karatsuba_sqr.o \
bn_mp_sqr.o bn_mp_div.o bn_mp_mod.o bn_mp_add_d.o bn_mp_sub_d.o bn_mp_mul_d.o \
bn_mp_div_d.o bn_mp_mod_d.o bn_mp_expt_d.o bn_mp_addmod.o bn_mp_submod.o \
bn_mp_mulmod.o bn_mp_sqrmod.o bn_mp_gcd.o bn_mp_lcm.o bn_fast_mp_invmod.o bn_mp_invmod.o \
bn_mp_reduce.o bn_mp_montgomery_setup.o bn_fast_mp_montgomery_reduce.o bn_mp_montgomery_reduce.o \
bn_mp_exptmod_fast.o bn_mp_exptmod.o bn_mp_2expt.o bn_mp_n_root.o bn_mp_jacobi.o bn_reverse.o \
bn_mp_count_bits.o bn_mp_read_unsigned_bin.o bn_mp_read_signed_bin.o bn_mp_to_unsigned_bin.o \
bn_mp_to_signed_bin.o bn_mp_unsigned_bin_size.o bn_mp_signed_bin_size.o \
bn_mp_xor.o bn_mp_and.o bn_mp_or.o bn_mp_rand.o bn_mp_montgomery_calc_normalization.o \
bn_mp_prime_is_divisible.o bn_prime_tab.o bn_mp_prime_fermat.o bn_mp_prime_miller_rabin.o \
bn_mp_prime_is_prime.o bn_mp_prime_next_prime.o bn_mp_dr_reduce.o \
bn_mp_dr_is_modulus.o bn_mp_dr_setup.o bn_mp_reduce_setup.o \
bn_mp_toom_mul.o bn_mp_toom_sqr.o bn_mp_div_3.o bn_s_mp_exptmod.o \
bn_mp_reduce_2k.o bn_mp_reduce_is_2k.o bn_mp_reduce_2k_setup.o \
bn_mp_reduce_2k_l.o bn_mp_reduce_is_2k_l.o bn_mp_reduce_2k_setup_l.o \
bn_mp_radix_smap.o bn_mp_read_radix.o bn_mp_toradix.o bn_mp_radix_size.o \
bn_mp_fread.o bn_mp_fwrite.o bn_mp_cnt_lsb.o bn_error.o \
bn_mp_init_multi.o bn_mp_clear_multi.o bn_mp_exteuclid.o bn_mp_toradix_n.o \
bn_mp_prime_random_ex.o bn_mp_get_int.o bn_mp_sqrt.o bn_mp_is_square.o bn_mp_init_set.o \
bn_mp_init_set_int.o bn_mp_invmod_slow.o bn_mp_prime_rabin_miller_trials.o \
bn_mp_to_signed_bin_n.o bn_mp_to_unsigned_bin_n.o
$(LIBNAME): $(OBJECTS)
$(AR) $(ARFLAGS) $@ $(OBJECTS)
$(RANLIB) $@
- Make HPAPINE and HPGCC versions:
$ cd ~/hpgcc/pies/libtommath-0.41
$ make clean
(lots of output)
$ make
(lots more output)
ranlib libtommath.a (last line of output)
$ mv libtommath.a ../libtommath_local.a
$ make clean
(lots of output)
$ make -f Makefile.hpgcc
(lots more output)
arm-elf-ranlib libtommath.a (last line of output)
$ mv ../libtommath_local.a .
$ ls -l *.a
-rwxr-xr-x 1 egan None 157254 Jan 8 18:32 libtommath.a
-rw-r--r-- 1 egan None 143378 Jan 8 18:29 libtommath_local.a
LibTomMath is now built for HPAPINE and HPGCC.
Unbounded Spigot π
uspi takes one
argument: max number of digits.
1 #include <hpgcc49.h>
2 #include <hpgraphics.h>
3 #include <tommath.h>
4
5 #ifndef HPAPINE
6 extern unsigned int __heap_ptr,_heap_base_addr;
7 int freemem();
8 #endif
- Line 2: Include hpgraphics.h
for indicator support.
- Line 3: LibTomMath headers.
- Lines 5-8: If not using HPAPINE add support to query free memory.
10 int main()
11 {
12 mp_int q, r, t, k, n, l;
13 mp_int r1, n1;
14 mp_int temp1, temp2, rmd;
15 int numdigits = 0, loops = 0, start, end;
16 double maxdigits;
17 char buf[4];
18 FILE *fp;
19 char *filename = "uspi.txt";
20 #ifndef HPAPINE
21 int mem, lowmem = 0;;
22 #endif
- Lines 12-14: Define LibTomMath multiple-precision integers.
- Line 19: Output file name.
- Lines 20-22: If not using HPAPINE create variables for memory usage
and reporting.
24 maxdigits = sat_pop_real();
25 if(maxdigits < 1) {
26 sat_push_zint_llong((int)maxdigits);
27 sat_stack_push_string("PI digits must be > 0");
28 sat_push_real(1);
29 return(0);
30 }
31
32 if((fp = fopen(filename,"w")) == NULL) {
33 char errormsg[30];
34
35 sprintf(errormsg,"Cannot open: %s",filename);
36
37 sat_stack_push_string(errormsg);
38 sat_push_real(1);
39 return(0);
40 }
41
42 sys_slowOff();
43 clear_screen();
- Lines 24-30: Get maximum number of digits from stack. Like the
previous examples reals are used because HPAPINE has problems with popping
integers. Error if not > 0.
- Lines 32-40: Open uspi.txt
for output, if error, then report error and exit.
- Line 42: Full speed ahead.
- Line 43: Clear screen.
45 #ifndef HPAPINE
46 mem = freemem();
47 #endif
48 mp_init(&q);
49 mp_init(&r);
50 mp_init(&t);
51 mp_init(&k);
52 mp_init(&n);
53 mp_init(&l);
54 mp_init(&r1);
55 mp_init(&n1);
56 mp_init(&temp1);
57 mp_init(&temp2);
58 mp_init(&rmd);
59
60 mp_set_int(&q,1);
61 mp_zero(&r);
62 mp_set_int(&t,1);
63 mp_set_int(&k,1);
64 mp_set_int(&n,3);
65 mp_set_int(&l,3);
- Lines 45-47: If not using HPAPINE, then query free memory and save
as mem.
- Lines 48-65: Initialize LibTomMath integers.
67 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
68 start = sys_RTC_seconds();
69
70 while(numdigits < maxdigits) {
71 loops++;
72
73 mp_mul_d(&q,4,&temp1);
74 mp_add(&temp1,&r,&temp1);
75 mp_sub(&temp1,&t,&temp1);
76 mp_mul(&n,&t,&temp2);
77
78 if(mp_cmp(&temp1,&temp2) == MP_LT) {
79 mp_todecimal(&n, buf);
80 printf("%d",atoi(buf));
81 fprintf(fp,"%d",atoi(buf));
82 numdigits++;
83
84 if(numdigits % 33 == 0) {
85 fprintf(fp,"\n");
86 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
87 #ifndef HPAPINE
88 if(freemem() < 25000)
89 hpg_set_indicator(HPG_INDICATOR_BATTERY,HPG_COLOR_BLACK);
90 #endif
91 }
- Line 67: Turn on busy indicator (hour glass).
- Line 68: Start time.
- Line 70: Start loop. Loop until
maxdigits attained.
- Lines 73-76: Start calculating π.
Read the aforementioned paper for algorithm details.
- Lines 78-82: Do we have a digit?
If so, print it to screen and file.
- Lines 84-91: If a multiple of 33 digits
has been printed then put a newline in the output file. At mod 33 the
screen will wrap and could advance removing the indicators. To be safe
turn on the busy indicator (hour glass), and if free memory is below 25000
bytes then turn on the low battery indicator. In this case it is now the
low memory indicator.
93 mp_sub(&r,&temp2,&r1);
94 mp_mul_d(&r1,10,&r1);
95
96 mp_mul_d(&q,3,&temp1);
97 mp_add(&temp1,&r,&temp1);
98 mp_mul_d(&temp1,10,&temp1);
99 mp_div(&temp1,&t,&temp1,&rmd);
100 mp_mul_d(&n,10,&temp2);
101 mp_sub(&temp1,&temp2,&n1);
102
103 mp_mul_d(&q,10,&q);
104
105 mp_copy(&r1,&r);
106 mp_copy(&n1,&n);
107 }
108 else {
109 mp_mul_d(&q,2,&r1);
110 mp_add(&r1,&r,&r1);
111 mp_mul(&r1,&l,&r1);
112
113 mp_mul_d(&k,7,&temp1);
114 mp_add_d(&temp1,2,&temp1);
115 mp_mul(&temp1,&q,&temp1);
116 mp_mul(&r,&l,&temp2);
117 mp_add(&temp1,&temp2,&temp1);
118 mp_mul(&t,&l,&temp2);
119 mp_div(&temp1,&temp2,&n1,&rmd);
120
121 mp_mul(&q,&k,&q);
122 mp_add_d(&k,1,&k);
123 mp_mul(&t,&l,&t);
124 mp_add_d(&l,2,&l);
125
126 mp_copy(&r1,&r);
127 mp_copy(&n1,&n);
128 }
- Lines 93-128: Continue calculating π.
Read the aforementioned paper for algorithm details.
130 if(keyb_isAnyKeyPressed())
131 break;
132
133 #ifndef HPAPINE
134 if(freemem() < 25000 && lowmem == 0) {
135 lowmem = numdigits;
136 beep();
137 hpg_set_indicator(HPG_INDICATOR_BATTERY,HPG_COLOR_BLACK);
138 }
139
140 if(freemem() < 5000)
141 break;
142 #endif
143 }
- Lines 130-131: If a keystroke is detected then breakout of loop, but
not the application.
- Lines 133-142: If not using HPAPINE then check for low memory.
If below 25000 bytes, then set the lowmem
flag to the current number of digits, beep, and light up the low battery
(memory) indicator. If free memory fall below 5000 bytes, then breakout
of loop
or risk a hang/crash.
145 end = sys_RTC_seconds();
146 fclose(fp);
147
148 printf("\n\n");
149 printf("longest digit: %d digits\n",(int)(log10(256.0)*mp_unsigned_bin_size(&q)));
- Line 145: Save final time.
- Line 146: Close output file.
- Line 149: Compute and report the length of the longest digit.
q is always the longest.
150 #ifdef HPAPINE
151 printf(" bytes alloc: %d\n",
152 mp_unsigned_bin_size(&q) +
153 mp_unsigned_bin_size(&r) +
154 mp_unsigned_bin_size(&t) +
155 mp_unsigned_bin_size(&k) +
156 mp_unsigned_bin_size(&n) +
157 mp_unsigned_bin_size(&l) +
158 mp_unsigned_bin_size(&r1) +
159 mp_unsigned_bin_size(&n1) +
160 mp_unsigned_bin_size(&temp1) +
161 mp_unsigned_bin_size(&temp2) +
162 mp_unsigned_bin_size(&rmd)
163 );
164 #else
165 printf(" bytes free: %d\n",mem);
166 printf(" bytes used: %d\n",mem-freemem());
167 if(lowmem)
168 printf(" bytes low(d): %d\n",lowmem);
169 #endif
- Lines 150-164: If using HPAPINE then add up the copy size of
the variables and report the minimum memory usage. The copy size
is the amount of RAM needed to copy a variable and not necessarily the size
the variable is currently using.
- Lines 165-169: If not using HPAPINE then report the starting free
memory and the memory used. If the low memory warning threshold was
reached then report the number of π digits
computed at the time the warning threshold was reached.
170 printf(" time(s): %d\n",end-start);
171 printf(" digits: %d\n",numdigits);
172 if(end-start == 0)
173 printf(" digits/s: NAN\n");
174 else
175 printf(" digits/s: %.2f\n",(float)numdigits/(float)(end-start));
176 printf(" iterations: %d\n",loops);
177 if(end-start == 0)
178 printf("interations/s: NAN");
179 else
180 printf("interations/s: %.2f",(float)loops/(float)(end-start));
181
182 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_WHITE);
183 hpg_set_indicator(HPG_INDICATOR_BATTERY,HPG_COLOR_WHITE);
184
185 sat_push_real(0);
186 beep();
187 sys_slowOn();
188 WAIT_CANCEL;
189 return(0);
190 }
- Lines 170-180: Report more stats.
- Lines 182-183: Turn off indicators.
- Lines 185-189: Push 0 (OK) to stack, beep to alert user to pay
attention, slow down to conserve battery life, wait for ON (CANCEL), then
exit.
192 #ifndef HPAPINE
193 int freemem()
194 {
195 register unsigned int stack_ptr asm ("sp");
196 unsigned int base;
197
198 base=(__heap_ptr == 0)? _heap_base_addr:__heap_ptr;
199
200 return stack_ptr-base;
201 }
202 #endif
uspi Wrapper
%%HP: T(3)A(R)F(.);
\<<
\->NUM
:3: "EXTEND/USPI" EVAL
IF
THEN
DOERR
END
\>>
Yet another sparse wrapper in need of robustness.
Again its your turn.
Run It/Checkit
Run with:
<< 5000 USPI >> EVAL
The screen output should look like this:
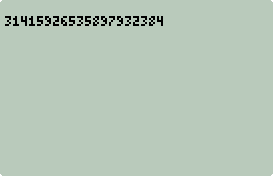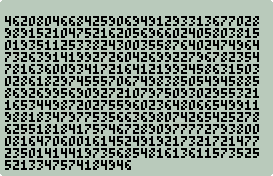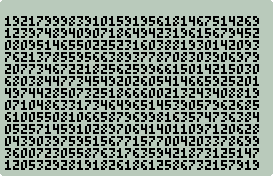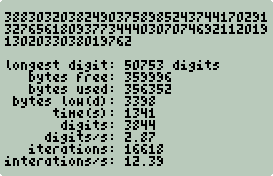
You'll notice that spigot
starts out slow and speeds up as the array traversals get shorter. This is
the bounded nature of the spigot algorithm. Conversely,
uspi starts out fast and gets slower,
much slower, as the integers dynamically allocate memory and get larger.
This is the unbounded nature of the unbounded spigot algorithm.
uspi only bounded by memory and your
patience.
After about 20 minutes (hang in there, listen to this while
you are waiting:
http://www.bbc.co.uk/radio4/science/5numbers2.shtml) the output should
look like this:
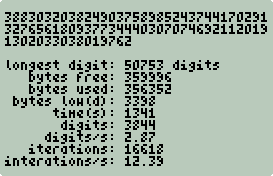
Memory free is very close to memory used. The low
memory warning was issued after 3398 digits were computed. You should have
noticed the "low memory" indicator and a low memory warning beep. When
memory was just about exhausted the loop ended only producing 3844 digits.
The longest integer digit used to compute π had 50753 digits and consumed at
least 21075 (50753/log10256) bytes of RAM.
Check with:
<< "USPI.TXT" CKPI >>
EVAL

Slow but accurate.
Breaking the 32373
Barrier
Part of the motivation for the Unbounded Spigot Algorithm
was the solve the problem of the Spigot Algorithm being unable to break past the
32373 barrier on 32 bit machines. Unfortunately there isn't enough memory
on the 50g to test this. However this can be tested with HPAPINE.
To try this out type:
$ cd ~/hpgcc/pies
$ make uspi_local
$ make ckpi_local
$ echo 40000 | ./uspi_local
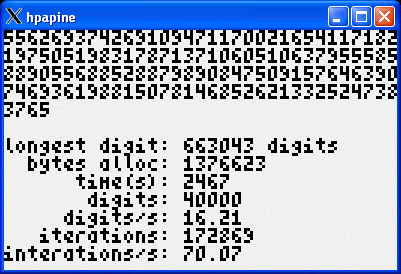
About 40 minutes later it completes. Notice the
length of the longest digit. That would have required over 275000 bytes of
memory just to store it. The 2nd longest digit is just about as long,
requiring a total of at least 550K of memory.
To prove this worked you still need to check it:
$ echo '"uspi.txt"' | ./ckpi_local
HPAPINE version 20071113_134757 (HPGCC 2.0)
Compiled on Sat Dec 8 18:45:20 MST 2007
CYGWIN_NT-5.1 1.5.24(0.156/4/2) i686 (oberon)
STRICT_HPGCC: no
GUI: GDK (X11)
--- Waiting for stack input on stdin...
--- Stack reading: done.
--- RPL Stack:
1: "uspi.txt"
--- RPL Stack:
3: "40000"
2: "40000"
1: " 0"
The 0 is the (OK). The 40000s are the number of
digits and the number of correct digits. This is processed by the
USPI wrapper. Wrapper code can
only be tested on the 50g. If you find a way to merge debug4x and HPAPINE
let me know.
|
Sidebar: Next Prime
I want to diverge just a bit to test one more LibTomMath
program: np (next prime).
np.c:
#include <hpgcc49.h>
#include <tommath.h>
int main()
{
mp_int a;
mp_err ret;
char *s, *buf;
int c;
sys_slowOff();
mp_init(&a);
s = sat_stack_pop_string_alloc();
if(s == NULL) {
sat_stack_push_string("Got NULL String!");
sat_push_real(1);
sys_slowOn();
return(0);
}
mp_read_radix(&a, s, 10);
if((ret = mp_prime_next_prime(&a, 5, 0)) != MP_OKAY) {
sat_stack_push_string(mp_error_to_string(ret));
sat_push_real(1);
sys_slowOn();
return(0);
}
mp_radix_size(&a, 10, &c);
buf = malloc(c * sizeof(char));
mp_toradix(&a, buf, 10);
sat_stack_push_string(buf);
sat_push_real(0);
sys_slowOn();
return(0);
}
This small C program will pop a digit string off the stack,
find the next prime number greater than the digit string and push back to the
stack the prime number as a string of digits.
Next Prime Wrapper
%%HP: T(3)A(R)F(.);
\<<
\->STR
:3: "EXTEND/NP" EVAL
IF
THEN
DOERR
END
OBJ\->
\>>
The np wrapper
takes an integer, converts to a string, calls
np then converts the return string to an integer. You can make this
more robust if you like.
Next Prime Shootout
Run both scripts:
<< 2 128 ^ NEXTPRIME >>
TIMER
<< 2 128 ^ NP >> TIMER
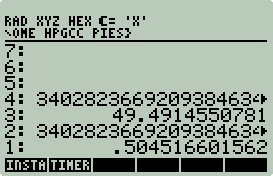
The internal 50g
NEXTPRIME didn't have a chance. The C version was almost 100 times
faster. Try it yourself. Then remove the timings and subtract the
values to verify that both got the same answer.
|
Machin
A π comparison can not be complete with out John
Machin's arctangent formula:
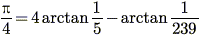
Like all the algorithms above some type of
multiple-precision library or code will be required. I wanted to try
something new, so I asked the Great Guide Google for guidance and was directed to
J.W. Stumpel's web site (http://www.jw-stumpel.nl/pi.html).
Stumpel's pi.c is short, fast, and portable.
I downloaded pi.c
and renamed it to pimach.c. I will comment
only on the changes that I made. No
changes to the algorithms were made. The complete source code is in
~/hpgcc/pies.
4 #include <hpgcc49.h>
5 #include <hpgraphics.h>
6
7 FILE *fp;
8 #ifndef HPAPINE
9 extern unsigned int __heap_ptr,_heap_base_addr;
10 #endif
11
12 int MAXSIZE;
13 int MAXDIGITS;
- Lines 4-5: Replaced stdio.h
with HPGCC headers. Normally stubs would have be used, but since this
program was heavily modified, there was no need to try to maintain
compatibility with future releases. BTW, this was released in 1991.
I do not think there will be future releases.
- Line 7: Pointer for output file.
- Lines 8-10: freemem()
support.
- Lines 12-13: Originally MAXSIZE
and MAXDIGITS were statically
assigned compile time variables. Now they are runtime assignable
variables.
44 int printbig(bignum number);
49 int atanbig(bignum A, unsigned int x);
50 int make_pi(void);
- Originally the above prototypes were
void. Now changed to int
to return malloc failures.
82 int printbig(bignum number)
83 {
84 bignum num;
85 int count = 0, ndigits = 0;
86
87 if((num = malloc(MAXSIZE*sizeof(int))) == NULL)
88 return(1);
89
90 copybig(num, number);
91 fprintf(fp,"%d.\n", num[0]);
92 while (ndigits < MAXDIGITS) {
93 num[0] = 0;
94 multbig(num, 100000);
95 fprintf(fp,"%05d", num[0]);
96 ndigits += 5;
97 count++;
98 if (count == 6) {
99 fprintf(fp,"\n");
100 count = 0;
101 }
102 }
103
104 return(0);
105 }
- Changes in bold. Before the size of
num was allocated at compile time.
Now num is dynamically allocated.
183 int atanbig(bignum A, unsigned int x)
184 {
185 bignum X, Y;
186 unsigned int n = 1;
187
188 if((X = malloc(MAXSIZE*sizeof(int))) == NULL)
189 return(1);
190 if((Y = malloc(MAXSIZE*sizeof(int))) == NULL)
191 return(1);
192
193 setbig(X, 1, 0);
194 divbig(X, x);
195 copybig(A, X);
196 x *= x;
197 while (1) {
198 n += 2;
199 divbig(X, x);
200 copybig(Y, X);
201 if (!divbig(Y, n))
202 break;
203 if (n & 2)
204 subbig(A, Y);
205 else
206 addbig(A, Y);
207 }
208
209 free(X);
210 free(Y);
211
212 return(0);
213 }
- Changes in bold. Same as above.
219 int make_pi(void)
220 {
221 bignum A, B;
222 int start, end;
223
224 if((A = malloc(MAXSIZE*sizeof(int))) == NULL)
225 return(1);
226 if((B = malloc(MAXSIZE*sizeof(int))) == NULL)
227 return(1);
228
229 printf("computing atan(1/5).....");
230 start = sys_RTC_seconds();
231 if(atanbig(A, 5) != 0)
232 return(1);
233 end = sys_RTC_seconds();
234 printf(" %3d s\n",end-start);
235
236 printf("computing atan(1/239)...");
237 start = sys_RTC_seconds();
238 if(atanbig(B, 239) != 0)
239 return(1);
240 end = sys_RTC_seconds();
241 printf(" %3d s\n",end-start);
242
243 multbig(A, 16);
244 multbig(B, 4);
245 subbig(A, B);
246 free(B);
247 if(printbig(A) != 0)
248 return(1);
249 printf("\n");
250
251 return(0);
252 }
- Lines 224-227, 251: Use malloc
instead of static compile assignment.
- Lines 229-241: Report time for each arctangent operation.
- Lines 231, 236, 247: atanbig
and printbig function (above) call
malloc, if a failure return as failed
to main. IANS pass any
malloc failures to
main.
254 #ifndef HPAPINE
255 int freemem()
256 {
257 register unsigned int stack_ptr asm ("sp");
258 unsigned int base;
259
260 base=(__heap_ptr == 0)? _heap_base_addr:__heap_ptr;
261
262 return stack_ptr-base;
263 }
264 #endif
- If not using HPAPINE add support for
freemem().
266 int main(void)
267 {
268 int start, end, speed;
269 char *filename = "pimach.txt";
270 #ifndef HPAPINE
271 int mem;
272
273 mem = freemem();
274 #endif
- All of main was completely
rewritten.
- Lines 270-274: If not using HPAPINE query the amount of unused
memory.
275 speed = sat_pop_real();
276 if(speed != 0 && speed != 1) {
277 sat_push_zint_llong(speed);
278 sat_stack_push_string("speed must be 0 or 1");
279 sat_push_real(1);
280 return(0);
281 }
282
283 MAXDIGITS = sat_pop_real();
284 if(MAXDIGITS < 1) {
285 sat_push_zint_llong(MAXDIGITS);
286 sat_stack_push_string("PI digits must be > 0");
287 sat_push_real(1);
288 return(0);
289 }
290 MAXSIZE = MAXDIGITS * 0.1038 + 10;
- Lines 275-281: Pop off the stack the speed. 0 for slow, 1 for
fast.
- Lines 283-290: Pop off the stack the number of digits to compute.
292 if((fp = fopen(filename,"w")) == NULL) {
293 char errormsg[30];
294
295 sprintf(errormsg,"Cannot open: %s",filename);
296
297 sat_stack_push_string(errormsg);
298 sat_push_real(1);
299 return(0);
300 }
301
302 if(speed == 0)
303 sys_slowOn();
304 else
305 sys_slowOff();
- Lines 292-300: Open pimach.txt
for output.
- Lines 302-305: Set the speed.
307 clear_screen();
308 printf("Machin's Pi\n\n");
309
310 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
311 start = sys_RTC_seconds();
312 if(make_pi() != 0) {
313 sys_slowOn();
314 sat_stack_push_string("Failed to allocate memory.");
315 sat_push_real(1);
316 return(0);
317 }
318 end = sys_RTC_seconds();
319 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_WHITE);
320
321 fclose(fp);
- Lines 307-310: Clean screen, print header, turn on busy indicator.
- Lines 311,318: Collect start and end time.
- Lines 312-317: Compute π, if
make_pi
returns not zero then a malloc
call failed.
- Line: 321: Close output file.
323 if(speed == 0)
324 printf(" speed: normal\n");
325 else
326 printf(" speed: fast\n");
327 printf(" time(s): %d\n",end-start);
328 printf("bytes alloc: %d\n",4*MAXSIZE*(int)sizeof(int));
329 #ifndef HPAPINE
330 printf(" bytes used: %d\n",mem-freemem());
331 #endif
332
333 sat_push_real(0);
334 beep();
335 sys_slowOn();
336 WAIT_CANCEL;
337 return(0);
338 }
-
Lines 323-331: Print stats.
-
Lines 333-337: Push 0 (OK) to stack, beep to alert
user, slow down to save batteries, wait for ON (CANCEL), exit.
Machin Wrapper
%%HP: T(3)A(R)F(.);
\<<
"Usage: Number PI Digits >0, Speed: 0|1" \-> u
\<<
DEPTH
IF 2 <
THEN u DOERR
END
\->NUM SWAP \->NUM SWAP DUP2 TYPE SWAP TYPE +
IF
THEN
u DOERR
END
:3: "EXTEND/PIMACH" EVAL
IF
THEN
DOERR
END
\>>
\>>
The stack must have two numbers or fail with, "Usage:
Number PI Digits >0, Speed: 0|1".
Run It/Check It
Run it:
<< 5000 1 PIMACH >> EVAL
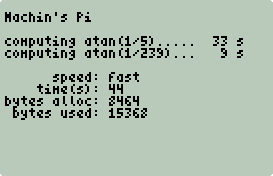
Check it:
<< "PIMACH.TXT" CKPI >>
EVAL

Yet another new record. 5000 correct digits in 44 seconds.
2 seconds faster than spigot and 1/5th
the memory!
More Arctangents: Euler, Gauss, Takano, Størmer,
et al
The Machin result was unexpected. And, since there
are other arctangent formulas that are known to be more efficient that Machin,
it's worth trying a few out. Instead of creating a different arctangent
program for each formula, I took pimach.c
and create a generic piatan.c.
I will only comment on the differences between
pimach.c and
piatan.c.
13 typedef struct tAtans {
14 signed int c;
15 unsigned int a;
16 } Atans;
189 int atanbig(bignum A, unsigned int x)
190 {
191 bignum X, Y;
192 unsigned int n = 1;
193 int xx = 1;
194
195 if((X = malloc(MAXSIZE*sizeof(int))) == NULL)
196 return(1);
197 if((Y = malloc(MAXSIZE*sizeof(int))) == NULL)
198 return(1);
199
200 setbig(X, 1, 0);
201 divbig(X, x);
202 copybig(A, X);
203 if(x < 65536) {
204 x *= x;
205 xx = 0;
206 }
207 while (1) {
208 n += 2;
209 divbig(X, x);
210 if(xx)
211 divbig(X, x);
212 copybig(Y, X);
213 if (!divbig(Y, n))
214 break;
215 if (n & 2)
216 subbig(A, Y);
217 else
218 addbig(A, Y);
219 #ifndef HPAPINE
220 if(keyb_isAnyKeyPressed())
221 beep();
222 #endif
223 }
224
225 free(X);
226 free(Y);
227
228 return(0);
229 }
-
atanbig had to be
altered to support denominators greater than 65535. Initially
atanbig just executed line 204 (x = x2).
This is a problem for 32 bit integers. Integers greater than 65535 squared
require more that 32 bits. To address this
divbig(X, x) is executed twice if the
denominator is > 65536. This does impact performance a bit.
-
Lines 219-222: If you not using HPAPINE check for a key
press. If pressed, then beep. Of all the π programs in this example
only this one can produce over 100,000 digits, but it takes hours. How do
you know if your 50g is working or hung? This no impact statement will
beep if a key is held down. Just a way to check that all is well.
The malloc checks really do work, so,
if no error, it should be working, but it human nature to want to check up on
a long running process.
232 int make_pi(int i,Atans *atans)
245 for(j=0;j<i;j++) {
246 printf("computing atan(1/%d)",atans[j].a);
247 itoa(atans[j].a,buf,10);
248 for(k=0;k<7-strlen(buf);k++)
249 printf(".");
250 start = sys_RTC_seconds();
251 if(atanbig(A, atans[j].a) != 0)
252 return(1);
253 end = sys_RTC_seconds();
254 printf("%5d s\n",end-start);
255
256 m = atans[j].c/abs(atans[j].c);
257 p = abs(atans[j].c);
258
259 multbig(A, p);
260
261 if(j == 0) {
262 copybig(B,A);
263 continue;
264 }
265
266 if(m == -1)
267 subbig(B, A);
268 else
269 addbig(B, A);
270 }
333 s = sat_stack_pop_string_alloc();
334
335 while(*s++ != '\0') {
336 if(*s == '{') {
337 s++;
338 k=0;
339 continue;
340 }
341 if(*s == '}') {
342 c[--k] = '\0';
343 if(k > 0) {
344 sscanf(c,"%d %d",&x,&y);
345 atans = (Atans *) realloc(atans, (i+1) * sizeof(Atans));
346 atans[i].c = x;
347 atans[i].a = y;
348 i++;
349 }
350 s+=3;
351 k=0;
352 continue;
353 }
354 c[k++] = *s;
355 }
-
In main a list of
arctangent constant and denominator pairs is popped of the stack and then parsed
and stored in an array (atans) using
the same list of lists function from csparse.c.
-
No error checking in this section. An exercise left
for the reader. E.g., check
s for
NULL.
364 printf("pi=");
365 for(k=0;k<i;k++) {
366 int m = atans[k].c/abs(atans[k].c);
367
368 if(k > 0)
369 if(m == 1)
370 printf("+");
371 printf("%d,%d",atans[k].c,atans[k].a);
372 pi_index += 1/log10(atans[k].a);
373 }
374 printf("\n\n");
piatan Wrapper
%%HP: T(3)A(R)F(.);
\<<
"Usage: Formula List, Number PI Digits >0, Speed: 0|1" \-> u
\<<
DEPTH
IF 3 <
THEN
u DOERR
END
ROT DUP TYPE
IF 5 \=/
THEN
UNROT u DOERR
END
\->STR UNROT
\->NUM SWAP \->NUM SWAP DUP2 TYPE SWAP TYPE +
IF
THEN
u DOERR
END
:3: "EXTEND/PIATAN" EVAL
IF
THEN
DOERR
END
\>>
\>>
This wrapper is a copy of
PIMACH altered to check for 3 arguments. Stack level 3 must contain
a list. The other two stack argument are the same as
PIMACH, i.e. number of digits and the
speed.
The list must be a list of arctangent constant and
denominator pairs. E.g. for Machin's formula:
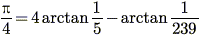
the list would be {{16
5}{-4 239}}. Notice how I multiplied the constants by 4. This
is not required if you are interested in computing π/4. Numerators other
than 1 are not supported. The denominators must be > 1. Sorry no
4*arctan(1) today.
piatan does not check for this (but
should), so use your wits. Denominators > 65535 should be avoided.
The arctangent code is different for denominators this large and performs a bit
slower.
Run It/Check it
Try the Størmer
formula:
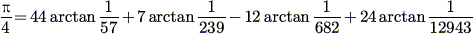
<< {{176 57}{28 239}{-48 682}{96 12943}} 5000
1 PIATAN >> EVAL
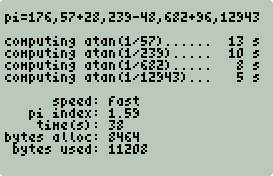
Check it:
<< "PIATAN.TXT" CKPI >>
EVAL

Wow, yet another record. 5001 digits in 38 seconds.
Below is a chart constructed from various arctangent π
formulas and piatan:
Originator
|
50g Formula |
π Index |
N=5000
Time(s)
|
N=10000
Time(s) |
N=100000
Time(s) |
| Euler, 1738 |
{{4 2}{4 3}} |
5.42 |
99 |
391 |
39100* |
| Hutton, 1776 |
{{8 3}{4 7}} |
3.28 |
76 |
300 |
30000* |
| Machin, 1706 |
{{16 5}{-4 239}} |
1.85 |
44 |
171 |
17100* |
| Gauss |
{{48 18}{32 57}{-20 239}} |
1.79 |
42 |
165 |
16500* |
|
Takano, 1982 |
{{48 49}{128 57}{-20 239}{48 110443}} |
1.78 |
45 |
173 |
17300* |
| Størmer, 1896 |
{{176 57}{28 239}{-48 682}{96 12943}} |
1.59 |
38 |
148 |
14800* |
*Estimated
The Takano and Størmer
arctangent formulas were used in 2002 by Yasumasa Kanada and team to calculate over 1.2
trillion π digits (ftp://pi.super-computing.org/README.our_latest_record).
A new (and current) world record.
The Takano formula did not out performed Gauss because of
the > 65535 denominator in the last term (110433). The arctangent code in
this example is less efficient with denominators > 65536.
All the arctangent algorithms scale as O(n2).
E.g. double the problem size, and the time to compute takes 4 times longer.
Current Standings
| Place |
Algorithm
|
AP/MP Library
|
Digits
|
Time(s)
|
Bytes Used |
| 5 |
Chudnovsky |
decNumber |
5006 |
375 |
Unknown |
| 4 |
Gauss AGM (Schönhage Variant) |
decNumber |
5005 |
122 |
31104 |
| 3 |
Spigot |
Internal |
5000 |
46 |
77092 |
| 6* |
Unbounded Spigot |
LibTomMath |
3844 |
1341 |
356352 |
| 2 |
Machin Arctangent |
Internal |
5001 |
44 |
15368 |
| 1 |
Størmer
Arctangent |
Internal |
5001 |
38 |
11208 |
*Disqualified for failure to compute 5000 digits.
One has to be careful when interpreting this data.
Algorithm, implementation, and problem size all have an impact on performance and memory usage. A good example of this is the recent world
record. Previously Chudnovsky and AGM-type algorithms have dominated
because of their efficiency. However, the new record set by Yasumasa
Kanada uses a less efficient arctangent formula, but makes up for it with a very
efficient implementation. This is probably the case with this 50g shootout as well. I suspect that the Chudnovsky and AGM programs performed
poorly because a general purpose AP library was used as apposed to custom
application specific internal code.
Chudnovsky Revisited
Before Størmer gets the
gold, I want to try a different Chudnovsky implementation. This time using
a very fast FFT by Takuya
Ooura.
Stefan Spännare's sspi source code and Takuya Ooura's FFT
can be obtained from:
http://www.spaennare.se/ssprog.html#chap4. The 50g version port is
quick and dirty, and that's all I will say. You can examine this 50g
version in the ~/hpgcc/pies/sspi
directory.
To build sspi,
type:
$ cd ~/hpgcc/pies/sspi
$ make clean
$ make sspi.hp
The sspi.hp binary
is huge (82K). To install sspi.hp,
just copy to the EXTEND directory on your SD card.
sspi Wrapper
%%HP: T(3)A(R)F(.);
\<<
\->NUM
:3: "EXTEND/SSPI.HP" RCL PrRUN
\>>
This bare bones wrapper differs from the rest in the
example in that RCL
PrRUN is used instead of
EVAL. This was necessary because
SSPI.HP was too big to convert to a
standalone executable.
SSPI.HP takes a
single real argument: power of 2 π digits.
E.g. 13 (213 = 8192) is required get at least 5000 digits.
Run It/Check It
Run it:
<< 13 SSPI >> EVAL
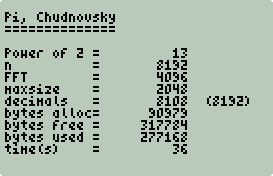
Check it:
<< "SSPI.TXT" CKPI >>
EVAL

8109 digits in 36 seconds. Chodnoveky bested Størmer
by 2 seconds.
And the Winner is...
| Place |
Algorithm
|
AP/MP Library
|
Digits
|
Time(s)
|
Bytes Used |
| 6 |
Chudnovsky |
decNumber |
5006 |
375 |
Unknown |
| 5 |
Gauss AGM (Schönhage Variant) |
decNumber |
5005 |
122 |
31104 |
| 4 |
Spigot |
Internal |
5000 |
46 |
77092 |
| 7* |
Unbounded Spigot |
LibTomMath |
3844 |
1341 |
356352 |
| 3 |
Machin Arctangent |
Internal |
5001 |
44 |
15368 |
| 2 |
Størmer
Arctangent |
Internal |
5001 |
38 |
11208 |
| 1 |
Chudnovsky |
FFT |
8109 |
36 |
277168 |
*Disqualified for failure to compute 5000 digits.
The gold for the the 5K sprint goes to the Chudnovsky Brothers. Do not let the 2 second
near win fool you, it wasn't even
close. It took Størmer 97 seconds to
compute the same 8109 digits.
Størmer picks up the
silver, and also takes the 100K and 200K gold:
100K Results
|
|
200K Results
|
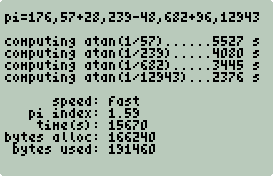
|
|
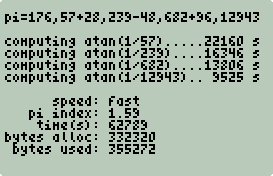
|
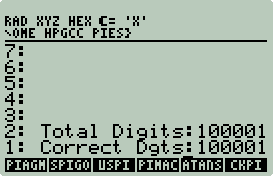
|
|
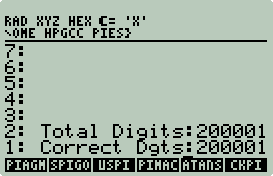 |
| 100,001 correct digits in 4.38 hours. |
|
200,001 correct digits in 17.44 hours. |
Only the arctangent formulas and implementations had the right speed and low
memory overhead to compute 100K and 200K digits. Low memory overhead was
also a factor in Yasumasa Kanada team's 1.2 trillion digit achievement.
Machin (the people's favorite) picks up the bronze.
ARM/C
vs. Saturn/Assembly, Machin vs. Machin, Mano-a-Mano
Early in this document I state emphatically that ARM/C is
faster than Saturn/Assembly. Is there proof? Are there two similar programs to compare? Thanks to Srpcic Silvo, there is. Srpcic
Silvo was kind enough to port his Saturn assembly π Machin program
to the 50g. This section will also answer a few questions that you may have asked yourself, "Why does
pimach have an option to run at slow and fast speed?",
and, "Why would I
ever want to run this type of computation slowly?" The answer to both
questions is the same; to have a fair comparison of ARM/C and Saturn/Assembly
performance on the 50g.
Digits
|
|
In this corner, weighing in at 1006 bytes:
Saturn/Assembly
|
|
In this corner, weighing in at 20834 bytes:
ARM/C
(with one arm tied behind his back,
i.e. sys_slowOn())
|
|
ARM/C
Speed Up |
| 100 |
|
3 seconds |
|
< 1 second |
|
> 3 |
| 500 |
|
45 seconds |
|
4 seconds |
|
11.25 |
| 1000 |
|
178 seconds |
|
12 seconds |
|
14.83 |
| 5000 |
|
4065 seconds |
|
271 seconds |
|
15 |
ARM/C was 15x faster. 92x if you run with
sys_slowOff(). The
Next Prime speed up was close to 100x.
The hpgcc.org
claims of 100x faster are true and expected since emulating a processor on a
small low-power handheld device is not going to perform at optimal speeds. Srpcic Silvo
reported that the 50g performance was only 50% faster that of the 48GX (266s for
1000 digits). Grim.
At least the C version does show an approximate performance doubling every 18
months from the 48GX release date to the 49g+ release date.
The source and binary for the Srpcic Silvo's Machin Saturn
code is in ~/hpgcc/pies/satasm.
To install just store Pi50g.hp in any
50g directory. Pi50g takes a single argument: number of π digits
to compute, and returns π as a string of digits. . The low battery warning flicker is your only
indication
that Pi50g is doing something. ON(CANCEL)
can be used to cancel the computation and return intermediate results.
TIMER,
S->F, and
CKPI will be needed to time and check
the results. I have confirmed that Pi50g
produces n+1 correct digits.
Summary
-
Writing this example couldn't have been easier, all the
code was just lying there, and its quiet easy to adapt existing C programs to the 50g.
-
Two different ARM/C vs. Saturn bakeoffs show that C code is
nearly 100 times faster than Saturn code.
-
Now you have a total of three new HPGCC libraries
(c9x-complex, CSparse, and LibTomMath).
Example: Computational Geometry Library
This example is a subset of a larger incomplete computational geometry
library. Someday I may have the time to complete it.
Unless stated otherwise all example code is in
~/hpgcc/cg. To build any example
type: make progname.hp. All
the examples were developed with HPAPINE, to test on your workstation type:
make progname_local. IMHO,
nothing adds more value to HPGCC than HPAPINE. Use it!
| 2D Convex Hull
A 2D convex hull is the smallest perimeter enclosing a set of points on a 2D
plane. The illustration to the right is example of a convex hull.
The crosses represent points or sites. The blue line is the convex
hull. The back circle is the center of gravity assuming that the area
bounded by the convex hull (blue line) is of uniform density. The
green square is the center of gravity for just the red points. This
pattern was generated by a simulation of 10,000 marbles being dropped.
The marbles were dropped one at a time with no collision checking
between marbles. A simulation of 10,000 dropping all at once and/or
checking for collisions is beyond the computational power of the 50g (in a
reasonable amount of time). The marble simulation and the colorful
hi-resolution bitmap were generated on the 50g. |
|
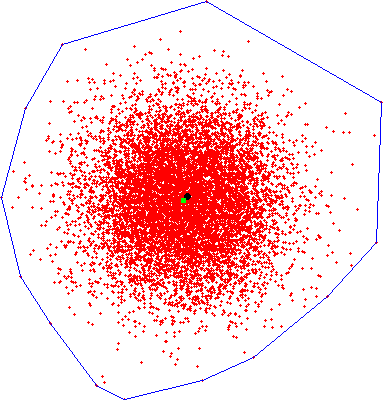 |
Marbles
The object of this simulation was to create a method that
could generate 1000s of points with a bias towards the center so that visual
examination of the convex hull would be easy. IOW, it is a test tool.
marbles takes a
single stack argument (number of marbles) and creates a text file (marbles.txt)
on the SD card with a space delimited pair of
x,y coordinates per line for each marble. E.g. 5 marbles:
-0.047152 0.889105
-0.193925 0.565576
0.058836 -1.436488
-0.515487 1.246967
-0.915515 -1.006480
Writing 10,000 marbles to SD can be slow. To keep the
user entertained, a graphical progress bar was implemented.
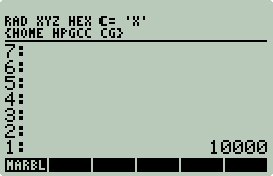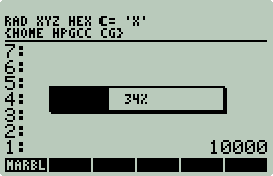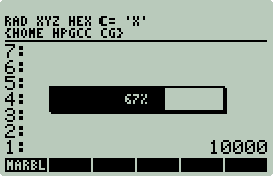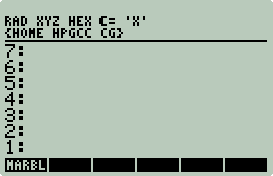
marbels.c:
1 #include <hpgcc49.h>
2
3 int progress(int, int, int, int);
4 int bar(int, int, int);
5 int intlog10(double);
6
7 int main(int argc, char *argv[])
8 {
9 int i;
10 double num;
11 FILE *fp;
12 int p=0, lp=0, li=0;
13 char errormsg[40], *filename="marbles.txt";
14
15 if((fp = fopen(filename,"w")) == NULL) {
16 sprintf(errormsg,"Cannot open: %s",filename);
17 sat_stack_push_string(errormsg);
18 sat_push_real(1);
19 return(0);
20 }- Lines 15-20: Open
marbles.txt for output or exit on
error.
22 num = sat_pop_real();
23 if(num < 1) {
24 sat_push_zint_llong((int) num);
25 sat_stack_push_string("Number of marbles must be > 0");
26 sat_push_real(1);
27 return(0);
28 }
29
30 sys_slowOff();
- Line 22: Pop number of marbles off the stack as a real.
HPAPINE has issues popping integers. It is also handy to use
->NUM in wrappers.
- Lines 23-28: Fail if less than one. It should really be 3, since you cannot calculate a convex hull without at least
3 points.
- Line 30: Full speed.
32 for(i=0;i<num;i++) {
33 double x, y;
34
35 x = gauss();
36 y = gauss();
37 fprintf(fp,"%0.6f %0.6f\n",x,y);
38
39 if(num > 300) {
40 p = ((i+1)*100)/num;
41 if(p > lp && i > (li + 50)) {
42 lp = p;
43 li = i;
44 progress(22,37,11,p);
45 }
46 }
47 if(keyb_isAnyKeyPressed())
48 break;
49 }
50 if(num > 300)
51 progress(22,37,11,100);
- Lines 35 and 36: gauss() is
a very handy function. It returns Gaussian random numbers. This is
the magic behind getting most of the marbles to be close to the center.
I.e., Independent random events often form a Gaussian (normal) distribution.
IOW, this simulation is not dropping 10,000 marbles, but is really dropping
one marble 10,000 times and marking the location.
- Lines 39-46: If the number of marbles is < 301 then skip the
progress bar. If > 300, then periodically display the progress bar.
Displaying the progress bar too frequently will just slow you down.
- Lines 41-45: Only update the progress bar after the percent changes
and at least 50 marbles have been dropped. This mix reduces the
overhead of the progress bar. And reduces flicker.
- Lines 47-48: Allow an impatient user to drop out of the
marble drop loop preserving intermediate results.
- Lines 50-51: All done, display 100%.
53 fclose(fp);
54 sat_push_real(0);
55 sys_waitRTCTicks(1);
56 sys_slowOn();
57 return(0);
58 }
- Lines 54-57: Close marbles.txt,
slow down, exit.
60 int progress(int x, int y, int length, int p)
61 {
62 unsigned char b[] = {0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01};
63 int l = length * 8 - 2;
64 int i;
65 char t[4];
66 static int shadow = 0;
67
68 if(shadow == 0) {
69 shadow = 1;
70 bar(x+1,y+1,length);
71 }
72
73 bar(x,y,length);
74
75 if(p < 0)
76 return(0);
77
78 if(p > 100)
79 p = 100;
80
81 sprintf(t,"%d%%",p);
82 print(t,131 - x*2 - 25 - 2*intlog10(p),y+4);
83
84 if(p == 0)
85 return(0);
86
87 for(i=0;i<(l*p)/100;i++) {
88 drawBlockXOR(b,11,x+i+1,y+1);
89 }
90
91 return(0);
92 }
- This is an example of the low level graphics functions available in HPGCC.
I do not recommend using them at all. It is too much work. This
graphics API uses bit patterns (sprites) that must be 8 bits wide and 1 or
more bits tall. To draw them to the screen you use OR/XOR.
- Line 62: Create a sprite of (12) 8 pixel lines with the last pixel
set.
- Lines 68-70: If drawing the progress bar the first time create a
shadow for the box.
- Line 73: Draw the initial bar.
- Lines 78-82: Put the % complete in the center of the bar.
- Lines 87-89: Use the sprite b
to create a vertical line 11 pixels tall and sweep it across the bar to the
correct % complete. The XOR provides the nice special effect of
reversing the video of the % digits as it sweeps by.
94 int bar(int x, int y, int length)
95 {
96 unsigned char b[] = {0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF};
97 unsigned char r[] = {0x7F,0x7F,0x7F,0x7F,0x7F,0x7F,0x7F,0x7F,0x7F,0x7F,0x7F,0x7F};
98 unsigned char m[] = {0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF,0xFF};
99 unsigned char l[] = {0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE};
100 int i;
101
102 for(i=0;i<length;i++) {
103 drawBlockOR(b,13,x+i*8,y);
104
105 if(i == 0)
106 drawBlockXOR(l,11,x+i*8,y+1);
107 else if(i == length-1)
108 drawBlockXOR(r,11,x+i*8,y+1);
109 else
110 drawBlockXOR(m,11,x+i*8,y+1);
111 }
112
113 return(0);
114 }
-
This code just draws an empty box with a one
pixel border around it.
-
Line 96: Define a sprite with all the
pixels set.
-
Line 97: Define a sprite with all but
the right bit set.
-
Line 98: Define a sprite with all bits
set.
-
Line 99: Define a sprite with all but
the left bit set.
-
Line 103: Draw a solid box (OR) 13
pixels tall. Length is in increments of 8 pixels.
-
Lines 106 and 108: XOR the left and right
pattern so that a single left and right line remain.
-
Line 110: XORs out the center.
-
Avoid this stuff and just use
hpgraphics.h.
116 int intlog10(double x)
117 {
118 int y=0;
119
120 x++;
121 while((x /= 10) > 1)
122 y++;
123
124 return(y);
125 }
Marbles Wrapper
%%HP: T(3)A(R)F(.);
\<< \-> n
\<<
n \->NUM
:3: "EXTEND/MARBLES" EVAL
IF
THEN
DOERR
END
"MARBLES.TXT"
\>>
\>>
-
Store the first stack element in local
variable n. If stack empty return
"Error: Too Few Arguments".
-
Convert n
to a real using ->NUM. If
->NUM cannot convert to real,
marbles will pop as 0 and error out.
-
Execute
marbles. If error call DOERR
and exit,
otherwise put the string "MARBLES.TXT"
on the stack.
Convex Hull 2D
ch2d is based on
the original
http://cm.bell-labs.com/who/clarkson/2dch.c written by Ken Clarkson.
ch2d
pops from the stack a single argument: filename containing points.
The file must be formatted with one pair of space delimited points per line,
e.g.:
-0.047152 0.889105
-0.193925 0.565576
0.058836 -1.436488
-0.515487 1.246967
-0.915515 -1.006480
While ch2d
is computing the hull, the message "Computing
Hull..." will be center printed on a blank screen. Computing the
hull for 10,000 points takes about 5 seconds. When complete a plot of the
points and hull will be displayed:

To exit press ON(CANCEL). After exiting
the stack should have 7 new items:

Stack levels:
-
Hull center of gravity assuming that the area
bounded by the convex hull is of uniform density.
-
Point center of gravity assuming that each
point has the same mass.
-
Hull perimeter.
-
Hull area.
-
Number of points.
-
Hull points. This is a list of points.
Each list item is a single hull point.
-
Hull GROB. This is a snapshot of the
plot displayed at the end of the hull computation.
I will only comment on the HPGCC specific
parts of ch2d.c:
30 #include <hpgcc49.h>
31 #include <hpgraphics.h>
143 int plotit(int n, int m, int v[], int art)
144 {
145 int i;
146 int x, y, xl, yl, xf, yf;
147 float w = bb_r - bb_l;
148 float h = bb_t - bb_b;
149 float scale;
150
151 xl = yl = xf = yf = 0;
152
153 hpg_clear();
- plotit is call from
main after the hull is computed.
- Lines 147 and 148: Compute the width and height of the hull.
- Line 153: Clear the screen.
155 if(w / h > 131.0 / 80.0)
156 scale = 130.0 / w;
157 else
158 scale = 79.0 / h;
- Lines 155-158: Determine (if using square pixels) if the hull would
fit best stretched vertically or horizontally, e.g.:
Points:
|
-1 0
1 0
0 2
0 -2 |
|

|
Points:
|
-2 0
2 0
0 1
0 -1 |
|
 |
The above two shapes are exactly the same, same area, same perimeter, same
shape. All that is different is that the x and y coordinates were
swapped and a different scale factor was used to maximize screen usage.
If the object is mostly square or circular then it will make
little difference.
160 for(i = 0; i < n; i++) {
161 if(art == 0) {
162 x = (points[i][0] - bb_l) * scale;
163 x += (130 - w * scale) / 2;
164 y = (points[i][1] - bb_b) * scale;
165 y += (79 - h * scale) / 2;
166 } else {
167 x = ((points[i][0] - bb_l) / w) * 130;
168 y = ((points[i][1] - bb_b) / h) * 79;
169 }
170 y = 79 - y;
171
172 hpg_draw_pixel(x, y);
173 }
- Lines 160-173: Plot the points.
- Lines 161-165: If the aspect ratio type (art)
= 0, then use square pixels. I.e. the diagram should represent the
position of each point using a 1:1 aspect ratio. The scale factor above
will be used to get maximum screen usage.
- Lines 167-168: If the aspect ratio type (art)
!= 0, then exaggerate the plot to all edges for maximum screen usage.
E.g.:
| art = 0 |
|
art = 1
|
 |
|
 |
- Line 172: Draw a pixel.
175 for(i = 0; i < m; i++) {
176 if(art == 0) {
177 x = (points[v[i]][0] - bb_l) * scale;
178 x += (130 - w * scale) / 2;
179 y = (points[v[i]][1] - bb_b) * scale;
180 y += (79 - h * scale) / 2;
181 } else {
182 x = ((points[v[i]][0] - bb_l) / w) * 130;
183 y = ((points[v[i]][1] - bb_b) / h) * 79;
184 }
185 y = 79 - y;
186
187 if (i == 0) {
188 xf = xl = x;
189 yf = yl = y;
190 continue;
191 }
192
193 hpg_draw_line(xl, yl, x, y);
194
195 xl = x;
196 yl = y;
197 }
198 hpg_draw_line(xl, yl, xf, yf);
199
200 return (0);
201 }
-
Lines 175-198 are like lines 160-173 except
that they plot the hull lines.
-
Line 193: Draw a hull line.
-
Line 198: Connect the last hull line
with the first hull line closing the hull.
203 int snapshot(char *grob)
204 {
205 char hex[1];
206 int g, t, x, y;
207
208 sprintf(grob, "GROB 131 80 ");
209
210 for(y = 0; y < 80; y++) {
211 g = 1;
212 t = 0;
213 for(x = 0; x < 131; x++) {
214 char p;
215
216 if((p = hpg_get_pixel(hpg_stdscreen, x, y)))
217 t += g;
218
219 g *= 2;
220
221 if(g == 16) {
222 sprintf(hex, "%X", t);
223 strcat(grob, hex);
224 g = 1;
225 t = 0;
226 }
227 }
228 sprintf(hex, "%X", t);
229 strcat(grob, hex);
230 sprintf(hex, "%X", 0);
231 strcat(grob, hex);
232 }
233
234 return (0);
235 }
-
Finally the answer to the question that you
have been asking yourself from the start, "How did he take all those screen
shots?"
HPGCC screens cannot be captured with ON-UpArrow. You must code your
application to capture them for you.
snapshot is just one of four different ways screen shots have been taken
for this article.
There are two different GROB formats: binary and
text. snapshot uses the text
format; it is easy to understand, develop code for, and push to the stack.
Read the HP48 FAQ if you want the details of the GROB text format.
-
Lines 210-231: Go from line to line,
pixel to pixel and get the pixel status (line 216). After a nibble (4
bits) has been collected, append the nibble to the GROB string.
-
Line 216: Pixel check. If 0, then
white or no pixel. If not 0, then black. Pixels can have 16
different values or shades of gray. GROBs are black and white, so any
color (shade of gray) is black.
237 int main(int argc, char *argv[])
238 {
239 int n, m, i;
240 #ifndef HPAPINE
241 char *hullpoints, grob[2740];
242 SAT_LIST p;
243 #endif
244 char *filename;
245 double A = 0, CHx = 0, CHy = 0, PM = 0, CPx, CPy;
246 int *v, art;
247 SAT_STACK_ELEMENT e;
248 SAT_STACK_DATA d;
249
250 art = sat_pop_real();
251 if(art != 0 && art != 1) {
252 sat_push_zint_llong(art);
253 sat_stack_push_string("Aspect ratio type must be 0 or 1");
254 sat_push_real(1);
255 return(0);
256 }
- The original 4 line 2dch.c main
was replaced by this beast.
- Lines 250-256: Pop off as a real the aspect ratio type. 0 for
1:1, 1 for 131:80.
258 sat_get_stack_element(1, &e);
259 sat_decode_stack_element(&d, &e);
260
261 if(d.type == SAT_DATA_TYPE_STRING) {
262 filename = str_unquote(d.sval, '\'');
263 sat_stack_drop();
264 } else {
265 sat_stack_push_string("Missing Filename");
266 sat_push_real(1);
267 return (0);
268 }
- Check that next stack item is a string, if not return error. If so,
then save to filename and drop it from
that stack.
270 sys_slowOff();
271
272 hpg_clear();
273 hpg_set_font(hpg_stdscreen, hpg_get_bigfont());
274 hpg_draw_text("Computing Hull...", 15, 38);
275 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
276
277 n = read_points(filename);
278 if(n == 0) {
279 char errormsg[30];
280
281 sprintf(errormsg,"Cannot open: %s",filename);
282 sat_stack_push_string(errormsg);
283 sat_push_real(1);
284 sys_slowOn();
285 return (0);
286 }
287 if(n < 3) {
288 sat_stack_push_string("Number of points must be > 2!");
289 sat_push_real(1);
290 sys_slowOn();
291 return (0);
292 }
- Line 270: Full speed ahead.
- Lines 272-275: Clear screen, set large font, draw text, set busy
(hourglass) indicator on.
294 m = ch2d(P, n);
295 v = hull_points(P, m);
- Call Ken Clarkson's original functions to calculate the convex hull.
297 for(i = 0; i < m; i++) {
298 double C, Px, Py;
299 int j = (i + 1) % m;
300 A += points[v[i]][0] * points[v[j]][1];
301 A -= points[v[i]][1] * points[v[j]][0];
302 C = ((points[v[i]][0] * points[v[j]][1]) -
303 (points[v[j]][0] * points[v[i]][1]));
304 CHx += (points[v[i]][0] + points[v[j]][0]) * C;
305 CHy += (points[v[i]][1] + points[v[j]][1]) * C;
306 Px = (points[v[j]][0] - points[v[i]][0]);
307 Py = (points[v[j]][1] - points[v[i]][1]);
308 PM += sqrt(Px * Px + Py * Py);
309 }
310 A /= 2;
311 CHx /= (6 * A);
312 CHy /= (6 * A);
313
314 CPx = points[0][0];
315 CPy = points[0][1];
316 for(i = 1; i < n; i++) {
317 CPx = (CPx * i + points[i][0]) / (i + 1);
318 CPy = (CPy * i + points[i][1]) / (i + 1);
319 }
- Compute center of gravity, area, and perimeter.
321 plotit(n, m, v, art);
322 #ifndef HPAPINE
323 snapshot(grob);
- Line 321: Plot the convex hull. Pass the number of points, the
number of hull points, the list of hull points, and the aspect ratio type.
- Line 323: Take a picture, it lasts longer. Store in
preallocated string grob (line 241).
325 if((hullpoints = malloc((50 * m + 4) * sizeof(char))) == NULL) {
326 sat_stack_push_string("Failed to allocate memory for hull points.");
327 sat_push_real(1);
328 return (0);
329 }
330 hullpoints[0] = '\0';
331 strcat(hullpoints, "{ ");
332 for(i = 0; i < m; i++) {
333 char point[50];
334 sprintf(point, "{ %0.12E %0.12E } ", points[v[i]][0],
335 points[v[i]][1]);
336 strcat(hullpoints, point);
337 }
338 strcat(hullpoints, " }");
- Convert the set of hull points to a string that resembles an RPL list of
lists.
340 sat_stack_push_string(grob);
341 sat_stack_push_string(hullpoints);
342 sat_push_zint_llong(n);
343 sat_stack_push_string("n");
344 sat_push_real(A);
345 sat_stack_push_string("Area");
346 sat_push_real(PM);
347 sat_stack_push_string("Perimeter");
- Line 340: Push out string GROB.
- Line 341: Push out string list of hull points.
- Lines 342-343: Push out number of points and tag.
- Lines 344-345: Push out area and tag.
- Lines 346-347: Push out perimeter and tag.
348 p = sat_list_create(20);
349 sat_list_add_real(p, CPx);
350 sat_list_add_real(p, CPy);
351 sat_push_list(p);
352 sat_list_destroy(p);
353 sat_stack_push_string("COG(p)");
- Create a new list 20 bytes long. Insert the point center of gravity
coordinates. Push the list to the stack. Free up the memory used
by the list. Push out a tag.
354 p = sat_list_create(20);
355 sat_list_add_real(p, CHx);
356 sat_list_add_real(p, CHy);
357 sat_push_list(p);
358 sat_list_destroy(p);
359 sat_stack_push_string("COG(h)");
- Create a new list 20 bytes long. Insert the hull center of gravity
coordinates. Push the list to the stack. Free up the memory used
by the list. Push out a tag.
360 sat_push_real(0);
361 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_WHITE);
362 beep();
363 sys_waitRTCTicks(1);
364 #endif
365 sys_slowOn();
366 WAIT_CANCEL;
367
368 return (0);
369 }
- Line 360: Push 0 to wrapper (i.e. OK, no errors).
- Line 361: Turn off busy indicator.
- Line 362: Notify user that computation and plot is complete.
- Line 365: Slow speed ahead.
- Line 366: Wait for ON(CANCEL).
Convex
Hull 2D Wrapper
%%HP: T(3)A(R)F(.);
\<< 0 \-> f art
\<<
f \->STR
art \->NUM
:3: "EXTEND/CH2D" EVAL
IF
THEN
DOERR
END
12 ROLL OBJ\->
12 ROLL OBJ\->
12 ROLLD
12 ROLLD
9 5 FOR i
\->TAG
i ROLLD
-1 STEP
\>>
\>>
-
Store the first two stack elements into local
variables f and
art. If short stacked return
"Error: Too Few Arguments".
Since, art
is hard coded as 0 (1:1 aspect ratio), only one stack argument (the filename
with the points) is required.
-
Convert f
to a string using ->STR.
-
Convert art
to a real using ->NUM.
-
Execute ch2d. If error call DOERR,
otherwise process the stack.
-
ch2d
will push 12 objects to the stack (13 if you count the return code, but that is
popped off by IF THEN DOERR END).
Stack levels 12 and 11 are the string versions of the snapshot (GROB), and the
list of hull points. The sequence << 12
ROLL OBJ-> 12 ROLL OBJ-> 12 ROLLD 12 ROLLD >> converts the strings to the
proper RPL objects and places them back in the correct positions.
-
The
<< 9 5 FOR i ->TAG i ROLLD -1 STEP >>
code does the match up. To do this with your own code, output to the stack
value, string tag pairs. Replace the
9 with
2*n-1 and the
5 with
n where
n is the number of pairs.
-
When the wrapper completes the output should
look like this:

|
Sidebar: P2F
All of the computational geometry programs in this example read files with one
(space delimited) 2D point per line. The RPL programmer may wish to write
code to create points to be used by these programs.
p2f was created to aid the RPL
programmer.
p2f is a simple utility that reads a
list of point pairs (as lists) and writes them to a file on the SD card in a
format that can be used by all the computational geometry programs in this
example.
p2f required two arguments:
list of point pairs, output file name.
For example say you wanted to use ch2d
to compute the area, perimeter, and center of gravity for a triangle with
vertices at (0,0),
(0,1), and
(1,0).
First you would push a list of point pairs:
{{0 0}{0 1}{1 0}}, then you would push
a file name: "TRI.TXT":
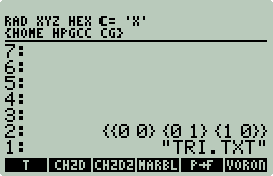
Next execute P->F, then put
"TRI.TXT" on the stack, and then run
CH2D:
Looks like a triangle defined by the following points:
(0,0),
(0,1),
(1,0).
Press
ON(CANCEL) to exit plot:
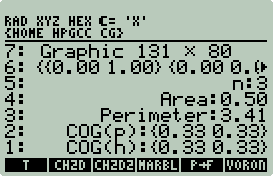
Voilà! Area, perimeter, and COG.
With UserRPL, p2f, and
ch2d, you can easily create program to
compute the area and perimeter of any regular polygon where the distance from
the center to the vertices is 1, e.g.:
%%HP: T(3)A(R)F(.);
\<< \-> n
\<<
1 n FOR i
2 \pi * n / i * \pi n / - DUP
SIN \->NUM SWAP
COS \->NUM NEG
2 \->LIST
NEXT
n \->LIST
\>>
"REGP.TXT" P\->F
"REGP.TXT" CH2D
DROP DROP
\>>
Example output:
Archimedes in c. 250 BC used n = 96 to accurately compute π to
2 decimal places. And so can you.
p2f.c:
1 #include <hpgcc49.h>
2 #include <hpstack.h>
- Line 2: Include hpstack.h.
HPStack will be used to process the list of lists in an elegant manor.
4 int main (void)
5 {
6 list_t *se, *t = NULL;
7 SAT_STACK_ELEMENT e;
8 SAT_STACK_DATA d;
9 int index=1;
10 double x, y;
11 char *filename, errormsg[40];
12 FILE *fp;
13
14 sat_get_stack_element(1,&e);
15 sat_decode_stack_element(&d,&e);
16
17 if (d.type == SAT_DATA_TYPE_STRING) {
18 filename = str_unquote(d.sval,'\'');
19 sat_stack_drop();
20 }
21 else {
22 sat_stack_push_string("Missing Filename");
23 sat_push_real(1);
24 return(0);
25 }
- Lines 14-25: This is getting old. Check for a string at stack
level one, but do not pop it. If a string, copy it and remove any single
quotes, point filename to it, drop it
from the stack. If not a string, error out.
27 if (hps_pop_list(&t) != HPS_OK) {
28 sat_stack_push_string("List of points missing");
29 sat_push_real(1);
30 return(0);
31 }
- Lines 27-31: Using HPStack pop a list off the stack or error out.
33 if((fp = fopen(filename,"w")) == NULL) {
34 sprintf(errormsg,"Cannot open: %s",filename);
35 sat_stack_push_string(errormsg);
36 sat_push_real(1);
37 return(0);
38 }
- Lines 33-38: Open filename
or error out.
40 sys_slowOff();
41
42 while(hps_list_get_list(t ,index++ ,&se) == HPS_OK) {
43 hps_list_get_real(se, 1, &x);
44 hps_list_get_real(se, 2, &y);
45
46 fprintf(fp,"%0.6f %0.6f\n",x,y);
47 }
48
49 fclose(fp);
50 sat_push_real(0);
51 sys_slowOn();
52 return (0);
53 }
P2F Makefile
The follow Makefile changes in bold
are necessary to compile p2f with
HPStack support:
export C_FLAGS = -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I../util -I hpstack -I hpparser -I hpgbmp \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD = arm-elf-ld
export LD_FLAGS = -L$(LIBS_PATH) -Lhpstack -Lhpparser -Lhpgbmp \
-T VCld.script $(LIBS_PATH)/crt0.o
export LIBS = -lhpgbmp -lstack -lparser -lhpg -lhplib -lgcc
Please read HPStack and HPParser on how to
install HPStack.
P2F Wrapper
%%HP: T(3)A(R)F(.);
\<< \-> p f
\<<
p
f \->STR
:3: "EXTEND/P2F" EVAL
IF
THEN
DOERR
END
\>>
\>>
-
Store the first two stack elements into local
variables p and
f. If short stacked return
"Error: Too Few Arguments".
-
It would not hurt to check that
p is actually a list. But, since
HPStack does this there is no critical need.
-
Convert f
to a string using ->NUM.
-
Execute f2p. If error call DOERR.
|
Convex Hull 2D II
ch2d2 is a modified version of
ch2d that is capable of creating hi
resolution binary GROBs and color bitmaps suitable for illustrations.
A comparison of ch2d and
ch2d2 output:
ch2d
131x80 GROB
|
ch2d2
320x320
GROB
|
ch2d2
320x320
bitmap
|
 |
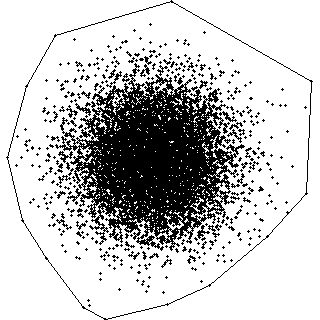 |
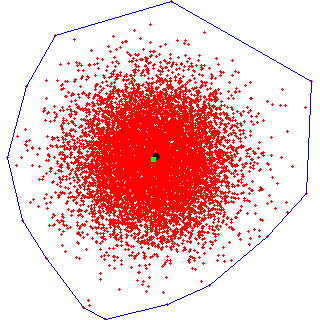 |
Larger images are possible:
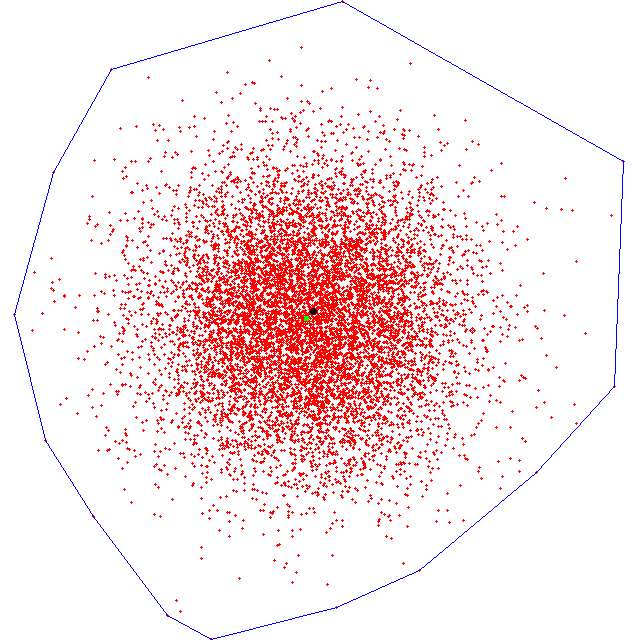
Only memory limits the size of the image.
ch2d2 requires 4
stack arguments: input filename, output filename, width,
height. The output filename must
have a .BMP or
.GRO extension in capital letters.
This is used to determine the type of graphic object to create.
Unlike ch2d,
ch2d2 does not provide a preview of the
plot. After hull, plot, and graphic object computation
ch2d2 pushes to the stack all the same
ch2d hull information. The plot
graphic is stored on the SD card using the output filename.
If the output file type is GROB (.GRO),
then the output file will be recalled to the stack by the wrapper.
Example ch2d2
sessions:
GROB Example
|
|
BMP Example |
|
|
|

|
|
 |

|
|

|
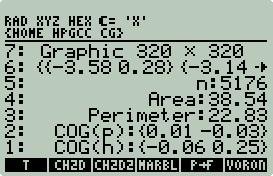 |
|
 |
The GROB is recalled to stack level 7 just like
ch2d.
marbles.gro is on the SD card as a
binary GROB object. |
|
The BMP is not recalled to stack.
marbles.bmp is on the SD card as a binary bitmap object. |
I will only comment on the on the differences between
ch2d.c and ch2d2.c:
30 #include <hpgcc49.h>
31 #include <hpgraphics.h>
32 #include <hpgbmp.h>
35 int W;
36 int H;
- Width and height are global variables popped from the stack. In
ch2d.c
values that presented W and
H were hard coded to 131 and 80.
146 int plotit(int n, int m, int v[], int art, hpg_t *image, double CHx, double CHy, double CPx, double CPy)
147 {
148 int i;
149 int x, y, xl, yl, xf, yf;
150 float w = bb_r - bb_l;
151 float h = bb_t - bb_b;
152 float scale;
153
154 xl = yl = xf = yf = 0;
155
156 hpg_clear_on(image);
157 hpg_set_color(image,HPG_COLOR_GRAY_13);
- plotit has 5 additional
arguments: off-screen image, COG(h) x y coordinates, and COG(p) x y
coordinates.
- Line 156: Clear off-screen image.
- Line 157: Set draw color. There are 16 colors or shades of
gray: HPG_COLOR_WHITE,
HPG_COLOR_GRAY_1 ...
HPG_COLOR_GRAY_14, and
HPG_COLOR_BLACK.
159 if(w / h > (float)W / (float)H)
160 scale = (W-1) / w;
161 else
162 scale = (H-1) / h;
163
164 for(i = 0; i < n; i++) {
165 if(art == 0) {
166 x = (points[i][0] - bb_l) * scale;
167 x += ((W-1) - w * scale) / 2;
168 y = (points[i][1] - bb_b) * scale;
169 y += ((H-1) - h * scale) / 2;
170 } else {
171 x = ((points[i][0] - bb_l) / w) * (W-1);
172 y = ((points[i][1] - bb_b) / h) * (H-1);
173 }
174 y = (H-1) - y;
175
176 hpg_draw_line_on(image,x+1, y, x-1, y);
177 hpg_draw_line_on(image,x, y+1, x, y-1);
178 }
179
180 for(i = 0; i < m; i++) {
181 if(art == 0) {
182 x = (points[v[i]][0] - bb_l) * scale;
183 x += ((W-1) - w * scale) / 2;
184 y = (points[v[i]][1] - bb_b) * scale;
185 y += ((H-1) - h * scale) / 2;
186 } else {
187 x = ((points[v[i]][0] - bb_l) / w) * (W-1);
188 y = ((points[v[i]][1] - bb_b) / h) * (H-1);
189 }
190 y = (H-1) - y;
191
192 if (i == 0) {
193 xf = xl = x;
194 yf = yl = y;
195 continue;
196 }
197
198 hpg_set_color(image,HPG_COLOR_GRAY_14);
199 hpg_draw_line_on(image,xl, yl, x, y);
200
201 xl = x;
202 yl = y;
203 }
204 hpg_draw_line_on(image,xl, yl, xf, yf);
- Lines 159-204 are the same as ch2d.c
except that the hard coded 131 and
80 have been replaced with
W and
H.
- Lines 176-177: Draw two intersecting lines to represent the point on
the off-screen image.
- Line 198: Set draw color to 14.
- Lines 199, 204: Draw the hull on the off-screen image.
206 hpg_set_color(image,HPG_COLOR_BLACK);
207 if(art == 0) {
208 x = (CHx - bb_l) * scale;
209 x += ((W-1) - w * scale) / 2;
210 y = (CHy - bb_b) * scale;
211 y += ((H-1) - h * scale) / 2;
212 } else {
213 x = ((CHx - bb_l) / w) * (W-1);
214 y = ((CHy - bb_b) / h) * (H-1);
215 }
216 y = (H-1) - y;
217 hpg_fill_circle_on(image,x,y,3);
218
219 hpg_set_color(image,HPG_COLOR_GRAY_12);
220 if(art == 0) {
221 x = (CPx - bb_l) * scale;
222 x += ((W-1) - w * scale) / 2;
223 y = (CPy - bb_b) * scale;
224 y += ((H-1) - h * scale) / 2;
225 } else {
226 x = ((CPx - bb_l) / w) * (W-1);
227 y = ((CPy - bb_b) / h) * (H-1);
228 }
229 y = (H-1) - y;
230 hpg_fill_rect_on(image,x-2,y-2,x+2,y+2);
231
232 return (0);
233 }
- Lines 206-217: Set the draw color to BLACK (15). Draw a circle
to represent the hull center of gravity.
- Line 217: Draw a solid circle with a radius of 3, pixel diameter of
7 (2*radius + 1(center point)).
- Lines 219-230: Set the draw color to 12. Draw a square to
represent the point center of gravity.
- Line 230: Draw a solid 5x5 pixel square.
235 int grobshot(char *filename, hpg_t *image)
236 {
237 int g, t, x, y;
238 unsigned char header[10], p;
239 unsigned long int length;
240 FILE *fp;
241
242 if((fp = fopen(filename,"wb")) == NULL) {
243 return(1);
244 }
- grobshot replaces the
ch2d.c
snapshot. It provides the same
functionality except that binary GROBs are created and written to SD and the
size is not fixed at 131x80.
- Line 242: Open filename for
binary writes.
246 fwrite("HPHP49-C",1,8,fp);
247
248 header[0] = 0x1e;
249 header[1] = 0x2b;
250
251 length = (int)ceil(W/8.0) * 2 * H + 15;
252
253 header[2] = (length & 0x0f) << 4;
254 header[3] = (length >> 4) & 0xff;
255 header[4] = (length >> 12) & 0xff;
256
257 header[5] = H & 0xff;
258 header[6] = (H >> 8) & 0xff;
259 header[7] = ((W & 0x0f) << 4) | ((H >> 16) & 0x0f);
260 header[8] = (W >> 4) & 0xff;
261 header[9] = (W >> 12) & 0xff;
262
263 fwrite(header,1,10,fp);
- Lines 246-263: Calculate and write out binary GROB header.
Google for HP48GROB.DOC for the binary GROB specification.
265 for(y = 0; y < H; y++) {
266 g = 1;
267 t = 0;
268 for(x = 0; x < W; x++) {
269 if((p = hpg_get_pixel(image, x, y)))
270 t += g;
271
272 g *= 2;
273
274 if(g == 256) {
275 fwrite(&t,1,1,fp);
276 t = 0;
277 g = 1;
278 }
279 }
280 if(g != 1)
281 fwrite(&t,1,1,fp);
282 }
283
284 fclose(fp);
285 return (0);
286 }
- Calculate and write out the binary GROB data. This method is much
faster than snapshot from
ch2d.c, and does not have any large
string to store in memory since the GROB is written directly to SD.
- Line 269: Get pixels from off-screen image.
288 int main(int argc, char *argv[])
289 {
290 int n, m, i, j;
291 char *hullpoints, *filename, *ofilename, *ofiletype, msg[40];
292 double A = 0, CHx = 0, CHy = 0, PM = 0, CPx, CPy;
293 int *v, art, grob=0, bmp=0;
294 #ifndef HPAPINE
295 SAT_LIST p;
296 #endif
297 SAT_STACK_ELEMENT e;
298 SAT_STACK_DATA d;
299 hpg_t *image;
300 FILE *fp;
301
302 art = sat_pop_real();
303 if(art != 0 && art != 1) {
304 sat_stack_push_string("Aspect ratio type must be 0 or 1");
305 sat_push_real(1);
306 return(0);
307 }
308
309 H = sat_pop_real();
310 if(H < 1) {
311 sat_stack_push_string("Height > 0");
312 sat_push_real(1);
313 return(0);
314 }
315
316 W = sat_pop_real();
317 if(W < 1) {
318 sat_stack_push_string("Width > 0");
319 sat_push_real(1);
320 return(0);
321 }
- Lines 302-307: Pop aspect ratio type.
- Lines 309-313: Pop height.
- Lines 316-321: Pop width.
323 sat_get_stack_element(1, &e);
324 sat_decode_stack_element(&d, &e);
325
326 if(d.type == SAT_DATA_TYPE_STRING) {
327 ofilename = str_unquote(d.sval, '\'');
328 sat_stack_drop();
329 } else {
330 sat_stack_push_string("Missing output filename");
331 sat_push_real(1);
332 return (0);
333 }
334
335 if(strlen(ofilename) > 4)
336 ofiletype = ofilename + strlen(ofilename) - 3;
337
338 if(strcmp(ofiletype,"GRO") == 0)
339 grob = 1;
340 if(strcmp(ofiletype,"BMP") == 0)
341 bmp = 1;
342
343 if(grob + bmp != 1) {
344 sat_stack_push_string("File ext. must be .GRO or .BMP");
345 sat_push_real(1);
346 return (0);
347 }
- Lines 323-333: Pop output filename.
- Lines 335-341: Obtain extension from output filename.
- Lines 343-346: Check for valid extension, if invalid error out.
349 sat_get_stack_element(1, &e);
350 sat_decode_stack_element(&d, &e);
351
352 if(d.type == SAT_DATA_TYPE_STRING) {
353 filename = str_unquote(d.sval, '\'');
354 sat_stack_drop();
355 } else {
356 sat_stack_push_string("Missing input filename");
357 sat_push_real(1);
358 return (0);
359 }
- Lines 349-359: Pop input filename.
361 sys_slowOff();
362
363 if((image = hpg_alloc_gray16_image(W,H)) == NULL) {
364 sprintf(msg,"Failed to allocate %dx%d image",W,H);
365 sat_stack_push_string(msg);
366 sat_push_real(1);
367 return(0);
368 }
- Lines 363-368: Allocate off screen image WxH 4 bit image. If
too big error out.
370 if((fp = fopen(ofilename,"w")) == NULL) {
371 sprintf(msg,"Cannot open: %s",ofilename);
372 sat_stack_push_string(msg);
373 sat_push_real(1);
374 return(0);
375 }
376 fclose(fp);
- Lines 370-376: Verify that the output filename can be written to.
The fclose is critical since the GROB
and BMP functions need to open the file. This code is not necessary
since checks for this take place later on, but I wanted a sanity check before
the screen was cleared and the hull computed.
377
...
424
- Lines 377-424: Compute hull, COG, area, and perimeter. Same
code as ch2d.c.
425 plotit(n, m, v, art, image, CHx, CHy, CPx, CPy);
426 hpg_clear();
427 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
- Line 425: Plot hull, hull point, and COGs.
- Line 426: Clear physical screen.
- Line 427: Turn on busy indicator (again since clear was called).
429 if(grob) {
430 hpg_draw_text("Computing GROB...", 15, 38);
431 if(grobshot(ofilename, image) == 1) {
432 sprintf(msg,"Cannot open: %s",ofilename);
433 sat_stack_push_string(msg);
434 sat_push_real(1);
435 return(0);
436 }
437 }
- If output file extension is .GRO
then compute a GROB. grobshot
should only fail if the output filename could not be opened for writing.
439 #define R 2
440 #define G 1
441 #define B 0
442
443 if(bmp) {
444 int ret, i;
445 palette_t mycolors[16];
446
447 for(i = 0;i < 16;i++)
448 for(j = 0;j < 4;j++)
449 mycolors[i].rgb[j] = 0x00;
- If output file extension is .BMP
then compute a bitmap. One of the nice features of HpgBmp is that you
can define 16 colors to replace the 16 shades of gray.
- Lines 445-449: Define a palette and set all 16 colors to white.
451 //background
452 mycolors[0].rgb[B] = 0xff;
453 mycolors[0].rgb[G] = 0xff;
454 mycolors[0].rgb[R] = 0xff;
455
456 //green COG(p)
457 mycolors[12].rgb[R] = 0x00;
458 mycolors[12].rgb[G] = 0xff;
459 mycolors[12].rgb[B] = 0x00;
460
461 //red sites
462 mycolors[13].rgb[R] = 0xff;
463 mycolors[13].rgb[G] = 0x00;
464 mycolors[13].rgb[B] = 0x00;
465
466 //blue CH
467 mycolors[14].rgb[R] = 0x00;
468 mycolors[14].rgb[G] = 0x00;
469 mycolors[14].rgb[B] = 0xff;
470
471 //black COG(h)
472 mycolors[15].rgb[R] = 0x00;
473 mycolors[15].rgb[G] = 0x00;
474 mycolors[15].rgb[B] = 0x00;
- Define replacement colors. This should be fairly obvious.
476 hpg_draw_text("Computing BMP...", 15, 38);
477 if((ret = hpg_save_anybmp_gray16(ofilename,mycolors,image,W,H)) != C_NoError) {
478 if(ret == C_ErrOpenFile)
479 sprintf(msg,"Cannot open: %s",ofilename);
480 if(ret == C_ErrMemory)
481 sprintf(msg,"Out of memory");
482 if(ret == C_ErrWritePalette)
483 sprintf(msg,"Unable to write palette");
484
485 sat_stack_push_string(msg);
486 sat_push_real(1);
487 return(0);
488 }
489 }
- Line 477: Compute and save bitmap. The function
hpg_save_anybmp_gray16 is a hacked up
version of hpg_save_bmp_gray16.
The differences are that
hpg_save_anybmp_gray16 will save a bitmap any off-screen image of any
size (including odd sizes), whereas
hpg_save_bmp_gray16 is limited to capturing the default screen and
saving it as a 132x80 bitmap. If
hpg_save_anybmp_gray16 fails, then error out with an HpgBmp error message.
491
...
533
- Lines 491-553: Same as ch2d.c
except that a string GROB is not pushed out to stack.
Convex Hull 2D II Makefile
ch2d2 uses a
modified version of Philippe Salmon's HpgBmp (http://phsalmon.club.fr/phsalmon/hpgbmp/hpgbmp.html)
library.
The follow Makefile changes in bold
are necessary to compile ch2d2 with HpgBmp support:
export C_FLAGS = -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I../util -I hpstack -I hpparser -I hpgbmp \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD = arm-elf-ld
export LD_FLAGS = -L$(LIBS_PATH) -Lhpstack -Lhpparser -Lhpgbmp \
-T VCld.script $(LIBS_PATH)/crt0.o
export LIBS = -lhpgbmp -lstack -lparser -lhpg -lhplib -lgcc
...
%_local: %.c
gcc -Wall -g -o $@ $< -DHPGCC -I $(HPAPINE)/include/ \
-I ../util -I hpgbmp \
-DHPAPINE -L $(HPAPINE)/lib/ -L hpgbmp \
-lhpgbmp_local -lhpapine \
$(shell pkg-config --libs gdk-2.0 gthread-2.0)
The modified version of HpgBmp is installed in ~/hpgcc/cg/hpgbmp including support for HPAPINE.
Convex Hull 2D II
Wrapper
%%HP: T(3)A(R)F(.);
\<< 0 \-> in out w h art
\<<
in \->STR
out \->STR
w \->NUM
h \->NUM
art \->NUM
:3: "EXTEND/CH2D2" EVAL
IF
THEN
DOERR
END
11 ROLL OBJ\-> 11 ROLLD
9 5 FOR i
\->TAG
i ROLLD
-1 STEP
out 3 \->TAG RCL DUP TYPE
IF 11 ==
THEN
7 ROLLD
ELSE
DROP
END
\>>
\>>
-
Store the first 5 stack elements into local
variables in,
out,
w,
h and
art. If short stacked return
"Error: Too Few Arguments".
Since, art
is hard coded as 0 (1:1 aspect ratio), only 4 stack arguments are required.
-
Convert in
to a string using ->STR.
-
Convert out
to a string using ->STR.
-
Convert w
to a real using ->NUM.
-
Convert h
to a real using ->NUM.
-
Convert art
to a real using ->NUM.
-
Execute ch2d2. If error call DOERR,
otherwise process the stack.
-
ch2d
will push 11 objects to the stack (12 if you count the return code, but that is
popped off by IF THEN DOERR END).
Stack level 11 is the string version of the
list of hull points. The sequence << 11
ROLL OBJ-> 11 ROLLD >> converts the string to the
proper RPL object and places it back to stack position 11.
-
The
<< 9 5 FOR i ->TAG i ROLLD -1 STEP >>
code does the match up. To do this with your own code, output to the stack
value, string tag pairs. Replace the
9 with
2*n-1 and the
5 with
n where
n is the number of pairs.
-
The << out 3
->TAG RCL DUP TYPE >> code will recall the binary graphic object.
-
The << IF 11
== THEN 7 ROLLD ELSE DROP END >> code will check for a binary GROB, if
true, then roll up into position 7 for stack output identical to
ch2d. If not a binary GROB drop
it from the stack.
GROB Stack Output
|
|
BMP Stack Output
|
 |
|
 |
This bullet point and the previous point can be dropped from the wrapper if you are
low on memory.
|
Sidebar: Screen Capture
Capture a GROB screen shot in 3 easy steps:
-
Include the ~/hpgcc/util/grobshot.h
file in your code, e.g.:
#include <grobshot.h>
-
Update your Makefile to search the
util directory for include files or
copy grobshot.h to your working
directory and use -I . (-I
space period), e.g.:
export C_FLAGS = -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I../util -I . -I hpstack -I hpparser -I hpgbmp \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
-
Take a picture with
grobshot(n), where is n is a number < 10000. The GROB
will be saved to SD as GROBnnnn.
E.g. if n = 1 then the file would be GROB0001,
e.g.:
grobshot(1);
Doing animations? Just increment n and call
grobshot(n)
repeatedly.
Capture a bitmap(BMP) screen shot in 4 easy steps:
-
Download HpgBmp from http://phsalmon.club.fr/phsalmon/hpgbmp/hpgbmp.html,
within your project directory, create a hpgbmp
subdirectory and extract the hpgbmp.zip
file in that directory.
-
Include the hpgbmp.h
file in your code, e.g.:
#include <hpgbmp.h>
-
Update your Makefile to search the
hpgbmp directory for include and library files,
and update LIBS to link-in
hpgbmp. , e.g.:
export C_FLAGS = -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I hpstack -I hpparser -I hpgbmp \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD = arm-elf-ld
export LD_FLAGS = -L$(LIBS_PATH) -Lhpstack -Lhpparser -Lhpgbmp \
-T VCld.script $(LIBS_PATH)/crt0.o
export LIBS = -lhpgbmp -lstack -lparser -lhpg -lhplib -lgcc
-
Take a picture with
hpg_save_bmp_gray16(name,NULL), where is name is a constant
string. The BMP
will be saved to SD as name,
e.g.:
hpg_save_bmp_gray16("foo123",NULL);
Doing animations? Create the following function in
your code:
int bmpshot(int n)
{
char name[12];
sprintf(name,"PIC%04d.BMP",n);
hpg_save_bmp_gray16(name,NULL);
return(0);
}
Just increment n and call
bmpshot(n)
repeatedly.
|
| Voronoi Diagrams
The illustration to the right is an example of a Voronoi diagram. Each
point represents a unique site. The lines define regions (cells)
associated with each site such that any point within the region is nearest
to the site within the region. There are many practical uses for Voronoi
diagrams:
- If each site presents a lookout tower, then the Voronoi diagram
defines the area nearest to each tower. E.g. forest fire lookout
towers.
- If each site presents a random forest fire, then the Voronoi diagram
lines would be the safest path out of the forest since they
maintain equal distance from any two nearest fires.
- Similar to the previous point, if a robot needed to compute the safest
obstacle avoidance path, then the Voronoi diagram lines would be used.
E.g. autopilot avoiding enemy radar.
- Many more nearest neighbor problems; nearest hospital, nearest school,
nearest pub, etc...
|
|
 |
The 50g Voronoi diagram code in this example is based on
Voronoi by Steven Fortune (http://cm.bell-labs.com/who/sjf)
and can be obtain from
http://cm.bell-labs.com/who/sjf/voronoi.tar. Voronoi is small
and fast; perfect for embedded programming.
The original Voronoi reads a list of input points
(sites), then outputs a plot or a plain text description (lines, points, and
vertices) of the diagram. The plot however is not suitable for navigation.
Since my goal was to create an interactive Voronoi application that could be
navigated from cell to cell, I had to make a number of additions to the
original. That said, I must admit I took the quick and dirty path.
Instead of completely changing the original, I just changed the output code to
create cell structures required for navigation. IOW, the original outputs
lines, points, and vertices, and I required polygons. This increases the
memory requirements per site ~2.5x because each vertex may belong to more than
one cell. A tradeoff that may increase interactive performance. Long
story short, you are limited to about 500 sites.
The 50g voronoi
pops from the stack a single argument: filename containing points.
The file must be formatted with one pair of space delimited points per line,
e.g.:
-0.047152 0.889105
-0.193925 0.565576
0.058836 -1.436488
-0.515487 1.246967
-0.915515 -1.006480
The Voronoi diagram computation takes seconds. After
the computation the entire Voronoi diagram is plotted, e.g.:
100 Random Points
|
|
500 Random Points |
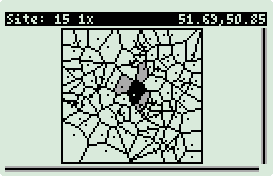 |
|
 |
The title bar displays the active site number, the
zoom factor, and the active site coordinates. The site number is the line
number of that site from the input file (base 0, i.e. the first site is site 0). In the center is the
view port, viewing the Voronoi diagram. The active site cell is black. The logical (based on
center of gravity) N, S, E, and W cell positions are gray. The scrollbars
at the bottom and right represent the relative position and zoom factor of the view
port.
In the event you run out of memory you will get the
following warning just before the diagram is computed:
In this event, voronoi
will continue to work with a subset of points.
Navigation Keys:
| Arrow Keys |
|
Move to the site N, S, E, or W. |
| + or - |
|
Increment or decrement zoom factor by 1. |
| * or / |
|
Multiple or divide zoom factor by 2. |
| 0 or SPC |
|
Set zoom factor to 1. |
| . (period) |
|
Auto-zoom. This handy function will
zoom in or out so that the active cell is clearly visible. |
| ENTER or I |
|
Site information, e.g.:
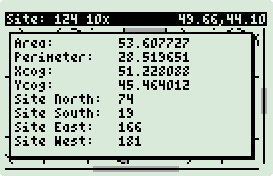
Press any key to exit site information. |
| ON(CANCEL) |
|
Exit application. |
| L |
|
Next site. E.g. if on site 4, jump
to site 5. |
| K |
|
Previous site. E.g. if on site 5,
jump to site 4. |
| S |
|
Produce a screen shot and a hi-resolution
diagram. After each image creation you will hear a beep.
The hour-glass will be present while the hi-resolution diagram is being
generated (takes time). The screen shot is saved on SD as
PICnnn.BMP and the
diagram as DIAnnn.BMP.
nnn starts at 0 and
increments by 1 each time S is pressed just before the snapshot is
taken. I.e. the first nnn
will be 001.
NOTE: The bitmaps used in this example were all generated
using this function. |
The animation below was captured while I navigated the
following 100 site diagram. On the left is what the 50g sees in memory,
and on the right is what the user sees.
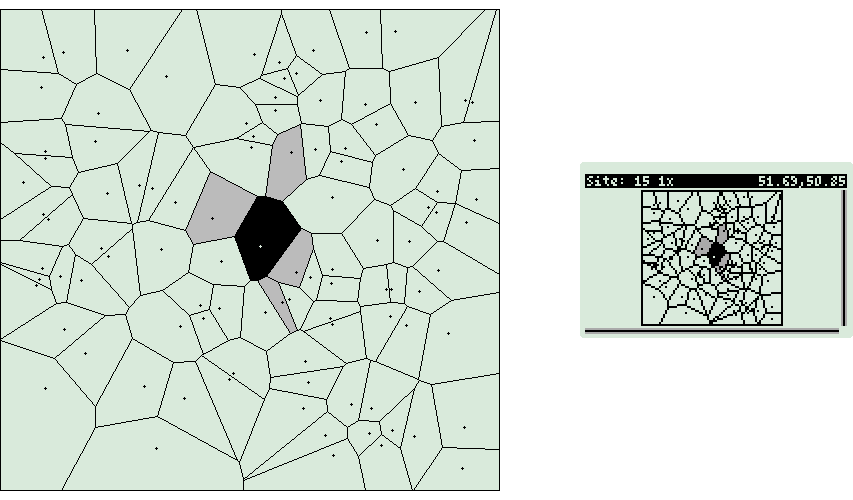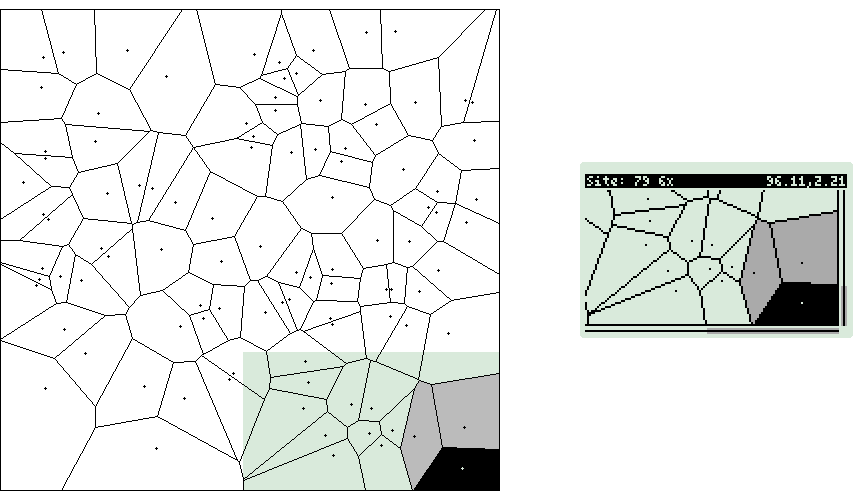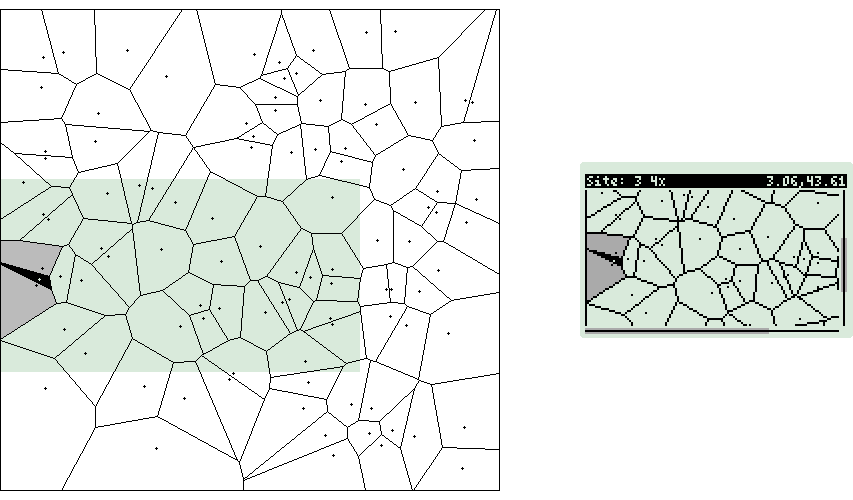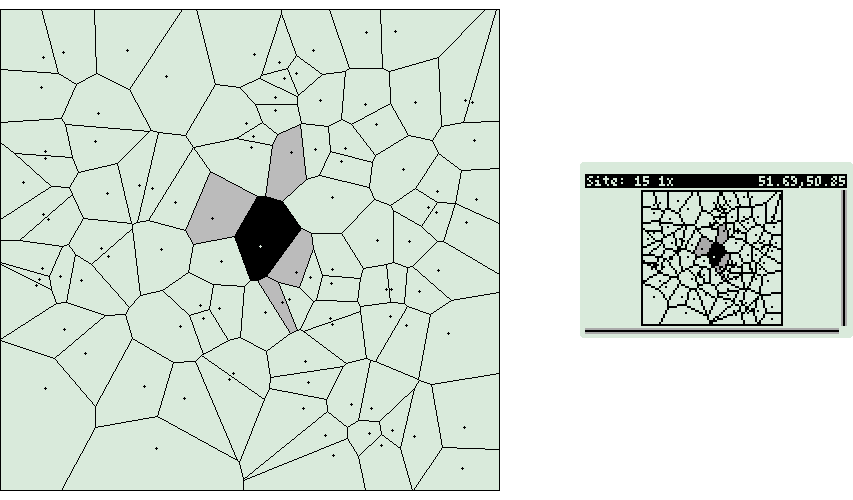
This is a large project compared to others in this
document. The project directory is ~/hpgcc/cg/voronoi.
To compile for the 50g type: make
voronoi.hp. To compile for HPAPINE type:
make voronoi_local. I must
emphasize that I could not have developed this without HPAPINE. Well I
could have, but it would have taken 10x more time and I would have lost
interest.
Because of the size of this project I will only comment on
HPGCC features that have not been discussed before. Specially all that is
new is keyboard input and double buffering.
main.c:
101 hpg_set_mode_gray4(1);
102 hpg_set_color(hpg_stdscreen, HPG_COLOR_BLACK);
103 hpg_set_font(hpg_stdscreen, hpg_get_bigfont());
104 hpg_clear();
105 hpg_flip();
106 hpg_clear();
107 hpg_flip();
-
Line 101: Set graphics mode to double buffer mode
with 4 shades of gray.
-
Line 102: Set drawing color to black.
-
Line 103: Set the drawing font size to big.
-
Line 104: Clear the other screen, not the screen you
are looking at.
-
Line 105: Switch the screen you are looking at with
the other screen. Lines 104 and 105 together clear the screen you are
looking at.
-
Lines 106-107: Repeat to ensure that both screens are
cleared. This is how double buffering works. All drawing operations
take place offline and then you call hpg_flip()
to quickly draw it all at once. hpg_flip()
is smart and will draw so that your interaction/animation is flicker free.
Alternatively you can draw to any off screen image, and use
hpg_blit() to copy it to
hpg_stdscreen.
hpg_blit() is used in my
draw() function to get around a bug
with lines and polygons that draw off screen and intersect the left side of the
screen.
After the diagram has been computed
interact is called.
interact is a big loop that captures
and processes keystrokes. When interact exits, control is return to
main,
main then pushes out a 0 (OK) status and exits.
351 int interact(Cell *cells, int nsites, PREC center) {
352 int zoom = 1, site = center;
353 PREC l, r, b, t;
354 PREC dx, dy;
355 PREC w = pxmax - pxmin;
356 PREC h = pymax - pymin;
357 PREC cx = (pxmax + pxmin)/2.0;
358 PREC cy = (pymax + pymin)/2.0;
359 PREC bb_l, bb_r, bb_b, bb_t;
360 int doinfo = 0, dosnap = 0, autozoom = 0;
- PREC is a macro defined in
vdefs.h that can be float or double.
To save memory floats are being used.
362 if(w/h > W/H) {
363 l = pxmin;
364 r = pxmax;
365 b = cy - w*((H/2)/W);
366 t = cy + w*((H/2)/W);
367 }
368 else {
369 b = pymin;
370 t = pymax;
371 l = cx - h*(W/(H*2));
372 r = cx + h*(W/(H*2));
373 }
374
375 draw(l, r, b, t, cells, nsites, site, zoom);
- Perform initial screen draw.
377 for(;;) {
378 sys_slowOn(); //conserve battery while user thinks
379 while(!keyb_isAnyKeyPressed())
380 ;
381 sys_slowOff(); //ok, got key, burn battery
- Line 377: Loop forever.
- Line 378: Slow down while waiting for input. No need to burn
batteries while user is or is not thinking.
- Lines 379-380: Loop until any key is pressed.
- Line 381: Got a key, speed up and process.
383 if(keyb_isON())
384 break;
385
386 if(keyb_isKeyPressed(0,5)) { // +
387 zoom++;
388 }
389 if(keyb_isKeyPressed(0,4)) { // -
390 zoom--;
391 if(zoom == 0)
392 zoom = 1;
393 }
394 if(keyb_isKeyPressed(0,2)) { // divide
395 zoom /= 2;
396 if(zoom == 0)
397 zoom = 1;
398 }
399 if(keyb_isKeyPressed(0,3)) { // *
400 zoom *= 2;
401 }
402 if(keyb_isKeyPressed(1,6) || keyb_isKeyPressed(3,6)) { // SPC
403 zoom = 1;
404 }
405 if(keyb_isKeyPressed(2,6)) { // .
406 autozoom = 1;
407 }
408 if(keyb_isUp()) {
409 if(cells[site].n != -1)
410 site = cells[site].n;
411 }
412 if(keyb_isDown()) {
413 if(cells[site].s != -1)
414 site = cells[site].s;
415 }
416 if(keyb_isLeft()) {
417 if(cells[site].w != -1)
418 site = cells[site].w;
419 }
420 if(keyb_isRight()) {
421 if(cells[site].e != -1)
422 site = cells[site].e;
423 }
424 if(keyb_isKeyPressed(7,1)) { // NXT
425 site++;
426 if(site == nsites)
427 site = nsites - 1;
428 if(zoom > 1)
429 autozoom = 1;
430 }
431 if(keyb_isKeyPressed(7,0)) { // STO
432 site--;
433 if(site < 0)
434 site = 0;
435 if(zoom > 1)
436 autozoom = 1;
437 }
438 if(keyb_isKeyPressed(6,5) || keyb_isKeyPressed(0,6)) // I or ENTER
439 doinfo = 1;
440 if(keyb_isKeyPressed(2,1)) // SIN
441 dosnap = 1;
- All of the above keyb_ statements
should be self explanatory. The not so obvious
keyb_isKeyPressed(x,y), where
x and
y are some key, can be decoded by
reading ~/hpgcc/2.0SP2/include/hpkeyb49.h.
There is a nice table with an entry for each key. IANS when the wait
for key loop exits you need to check for which key was pressed and act on
it.
443 if(autozoom) {
...
473 }
- Do the auto zoom code. All C, just computes the zoom.
478 if(zoom == 1) {
...
521 }
- This section draws the screen even if the screen did not change.
This is important since operations in doinfo
and dosnap need to update an existing
screen to be more aesthetic (e.g. info pop up box, or indicators). IOW,
if the screen changes, it gets written offline and flipped out. No
problem. If the screen does not change (display info or snapshot), then
redraw the screen to the other buffer. Both buffers will have exactly
the same screen. Now it is easy to write to the buffer and display a
change to the screen, to remove the change, just flip back.
523 if(doinfo) {
...
526 }
528 if(dosnap) {
529 int ret;
530
531 snapshot();
532 beep();
533 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_BLACK);
534 hpg_flip();
535 if(zoom == 1)
536 ret = drawdia(l, r, b, t, cells, nsites, site, DIA_W, DIA_H, snapshots);
537 else
538 ret = drawdia(bb_l, bb_r, bb_b, bb_t, cells, nsites, site, DIA_W, DIA_H, s
napshots);
539 if(ret == 0)
540 beep();
541 hpg_flip();
542 hpg_set_indicator(HPG_INDICATOR_WAIT,HPG_COLOR_WHITE);
543 hpg_flip();
544 dosnap = 0;
545 }
- Indicators like the rest of the screen have to be
hpg_flip()'d to appear.
- Line 533: Turn on the busy indicator in the buffered screen.
- Line 534: Display the indicator.
- Line 541: Flip the screen with the indicator back to the buffer.
- Line 542: Remove the indicator.
547 while(keyb_isAnyKeyPressed());
548 sys_waitRTCTicks(2); //fix key bounce
549 }
550
551 return(0);
552 }
- When the key was pressed at the top of the loop, the key press is
processed immediately, not when you release the key. HPGCC is so fast it
is possible to still have the key down after the key was processed and return
to the top of the loop and reprocess the key.
- Line 547: While the key is still down wait. Do not return to
top of loop until key is released.
- Line 548: Wait just a fraction of a second to fix key bounce
problems. When you press a key it is possible because of variability in
thresholds that it may look like it was pressed multiple times very quickly.
A small delay can fix this.
554 int draw(PREC l, PREC r, PREC b, PREC t, Cell *cells, int nsites, int site, int zoom) {
555 PREC w = r - l;
556 PREC h = t - b;
557 PREC scale;
558 int i;
559 hpg_t *image;
560 char sitename[20];
561 char pointname[20];
562
563 image = hpg_alloc_gray4_image(W+1,H);
564
565 hpg_clear();
566 hpg_clear_on(image);
567 hpg_clip(image,1,0,W+1,H);
- This is my draw function. It draws the entire screen, diagram, title
bar, and scrollbars.
- Line 563: Allocate off screen image with width one greater that
required. This image is not the double buffered image.
- Line 566: Clear the off screen image.
- Line 567: Set the clipping of the image so that the left most column
of pixels is clipped.
- The aforementioned is a hack for an HPGCC bug that improperly displays
lines that draw into the negative horizontal space. Not a problem for
vertical. To solve the problem I created an image one pixel wider and
clipped out the 0 column. Later I will copy this to the double buffer
and flip it.
569 if(w/h > W/H)
...
687 }
- Draw image in to offline image.
689 hpg_blit(image,1,0,W,H,hpg_stdscreen,0,8);
690 hpg_flip();
691 hpg_free_image(image);
692 return(0);
- Copy offline image to double buffer, flip it, and free up memory used by
offline image (important to avoid memory leaks).
Voronoi Makefile
This Makefile is unlike the others in that all of the C
code is compiled into a single executable. The previous Makefiles all had
a one to one relationship between source and executable. Changes in
bold:
export C_FLAGS = -mtune=arm920t -mcpu=arm920t \
-mlittle-endian -fomit-frame-pointer -msoft-float -Wall \
-Os -I$(INCLUDE_PATH) -I hpgbmp -I \
-L$(LIBS_PATH) -mthumb-interwork -mthumb
export LD = arm-elf-ld
export LD_FLAGS = -L$(LIBS_PATH) -L hpgbmp \
-T VCld.script $(LIBS_PATH)/crt0.o
export LIBS = -lhpgbmp -lhpg -lhplib -lgcc
- Link with a hacked up version of HpgBmp for screen shot and hi-resolution
diagrams. See the
ch2d2 example for details.
SRC = edgelist.c geometry.c heap.c main.c memory.c output.c voronoi.c
OBJ = $(SRC:%.c=%.o)
EXE = voronoi.exe
HP = voronoi.hp
$(EXE): $(OBJ)
$(LD) $(LD_FLAGS) $(OBJ) $(LIBS) -o $@
$(HP): $(EXE)
$(ELF2HP) -s100 $< $@
- Use the hard coded names and link with all objects.
voronoi_local: $(SRC)
gcc -Wall -g -o $@ $(SRC) -DHPGCC -I $(HPAPINE)/include/ -I hpgbmp \
-DHPAPINE -L $(HPAPINE)/lib/ -lhpapine \
-L hpgbmp -lhpgbmp_local \
$(shell pkg-config --libs gdk-2.0 gthread-2.0)
Voronoi Wrapper
%%HP: T(3)A(R)F(.);
\<< \-> f
\<<
f \->STR
:3: "EXTEND/VORONOI" EVAL
IF
THEN
DOERR
END
\>>
\>>
-
Convert the first stack item to a string (if there is a
stack item to convert), otherwise error with "Error:
Too Few Arguments".
-
Run vornoroi.
-
Report any errors, otherwise exit quietly.
Random Square/Circle
randsqr.c and
randcir.c are random point generators
that I used to test voronoi. The
source is located in ~/hpgcc/cg.
Random Square, 200 Points
|
|
Random Circle, 200 Points |
 |
|
 |
The square pattern is evenly spread out.
|
|
The circle pattern is more concentrated in the center. |
Wrapper%%HP: T(3)A(R)F(.);
\<< \-> n f
\<<
n \->NUM
f \->STR
:3: "EXTEND/RANDSQR" EVAL
IF
THEN
DOERR
END
\>>
\>>
|
|
Wrapper%%HP: T(3)A(R)F(.);
\<< \-> n f
\<<
n \->NUM
f \->STR
:3: "EXTEND/RANDCIR" EVAL
IF
THEN
DOERR
END
\>>
\>>
|
Computational
Graphics Library
Creating a library is the best way to share your creation
with the world.
-
On the 50g change to the
HOME/HPGCC/CG directory.
-
Define and store the following
variables (yes the $ (
 in ALPHA mode) is part of the
variable name):
in ALPHA mode) is part of the
variable name):
Variable
|
|
Value |
|
Description |
$TITLE
|
|
"CGLIB"
|
|
This is the title of the library. The first five
characters will be used for the name that is shown in the library menu (
 ). ).
|
$ROMID
|
|
1314
|
|
This is a number (real or integer) which must be unique
to your library. This allows the calculator to identify the library, and
should be in the range 769 to 1792.
|
$CONFIG
|
|
1
|
|
Default configuration:
ATTACH library at power on.
|
$VISIBLE
|
|
{CH2D CH2D2 REGP VORONOI P->F
MARBLES RANDCIR RANDSQR}
|
|
This is a list of the commands in the current directory
that you want to have visible in the library's menu.
List them in the order you want them to appear.
|
|
$EXTPRG |
|
'cgmenu'
|
|
This is the name the setup program that will be executed
each time the library is attached (e.g. at power on).
|
| $HIDDEN |
|
{cgmenu}
|
|
Items that need to be in the library, but are not visible
to the user. This is required for
$EXTPRG.
|
| cgmenu |
|
%%HP: T(3)A(R)F(.);
\<<
IF DUP 0. R~SB ==
THEN
SWAP LIST\-> 1 + DUP
R\->I \->STR ".Comp. Geometry" +
{
\<<
1314 MENU
\>>
}
+ SWAP \->LIST SWAP
END
\>>
|
|
This UserRPL script adds a "nn.Comp.
Geometry" menu item to the APPS
menu. Where nn is
the next menu number. Only modify the sections in bold:
- 0.: This is
the menu to add an item to. APPS
is menu 0. Refer to 49g+ AUR for a list of menus.
- ".Comp. Geometry":
This is the menu item description. The leading period is for the
menu number.
- 1314 MENU:
This is the code to execute when this menu item is selected.
This script is executed for each menu. If there is a match then
append to the menu the additional item.
NOTE: The R~SB
command is part of the development library, to access type:
256 ATTACH 256 MENU. |
- To create the library and store (not install) to SD card
type into the 50g:
256 ATTACH

CRLIB

:3:CG.LIB

Your stack should look like this:

Save to SD Card by pressing
 .
Your SD card now has an EXTEND
directory and an CR.LIB file.
If you wish to share your C code and wrappers then just zip up both
EXTEND and
CR.LIB as
CR.ZIP and distribute.
.
Your SD card now has an EXTEND
directory and an CR.LIB file.
If you wish to share your C code and wrappers then just zip up both
EXTEND and
CR.LIB as
CR.ZIP and distribute.
The
installation instructions are very simple (you can skip 1 and 2 since you
already have it on your 50g):
-
On your PC extract CR.ZIP into the root of the SD Card.
-
Insert SD Card into 50g.
-
Type into the 50g:
:3:CG.LIB


2


Now press
 ,
then press
,
then press  +
+ .
.
-
Test. Press APPS and scroll to the bottom of the
list:
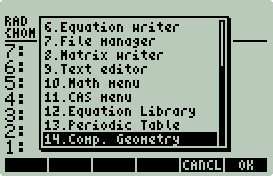
Select Comp. Geometry:
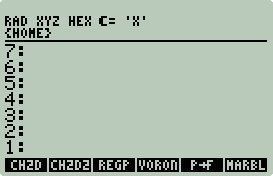
This menu can also be accessed with 1314 MENU
or with 
 .
.
The purge the directory.
-
Type:
:2:1314 PURGE
Tada! You now have a sharable Computational Geometry library.
Extend your 50g with C -
Part 3 - More Examples
Like Part 2, this section will also focus on learning by
example. However, unlike Part 2, only the interesting parts of the code
will be annotated. The reader is assumed to know how to compile C code with HPGCC, install binaries to SD, and create wrappers.
All of this
was covered in Part 1.
How to Follow the Examples
-
Each example will have specific instructions on how to
install each example.
-
$ prompts indicate
something you should type. The text to be entered will be in
bold courier and the output in
courier, e.g.:
$ hello
go away!
-
Files ending in
.c.nl are line numbered version of the
.c code. My comments will
reference line numbers. Line numbers were generated with:
perl -pi -e 's/\t/
/g' < program.c | nl -nln -ba >program.c.nl
-
All C programs will be in lowercase courier, e.g.
program. All RPL wrappers will be
in uppercase courier, e.g. PROGRAM.
-
To maintain consistency most code was reformatted with:
indent -kr -ts4 *.c *.h
The Examples
-
Viète Accelerated.
This example will demonstrate how to use libfsystem
with your SD card to read and write
an array too large to fit into memory, text cursor positioning, SD card
benchmarking, how to generate Excel 3D bar plots, and how to
generate dynamic UserRPL code to be processed after the C program exits.
Viète Accelerated
Introduction
In 1592 French mathematician François Viète (or Vieta) discovered the first exact formula for π [9]:
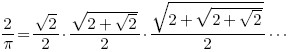 |
(1) |
This infinite product formula, while elegant, is a poor
choice for computing the decimal digits of π because it converges so slowly.
As illustrated in Table 1, 6 decimal digits are produced after 10
iterations. And, this ratio (10:~6) remains constant.
Table 1: Viète vs. Gauss AGM, number of π digits per iteration
|
| Iterations |
Viète |
Gauss AGM |
| 1 |
0 |
0 |
| 2 |
1 |
1 |
| 3 |
2 |
2 |
| 4 |
2 |
5 |
| 5 |
3 |
10 |
| 6 |
4 |
21 |
| 7 |
5 |
43 |
| 8 |
5 |
87 |
| 9 |
5 |
174 |
| 10 |
6 |
349 |
Glancing at Eq. 1, you may have observed that each Viète iteration requires a
square root operation. Square root operations are computationally very
expensive making Viète's Formula computationally uninteresting.
For me, that changed in June 2008. An article by Rick Kreminski [10]
sparked my interested in Vieta's Formula again. Kreminski offers a
recursion that accelerates the convergence of Viète's Formula.
Of course the first thing that occurred to me was to try it on my 50g.
Viète became computationally interesting.
Kreminski's Viète recursion formula [10]:
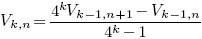 |
(2) |
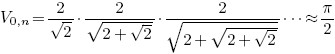 |
(3) |
Beautifully simplistic! But not so simple to implement.
NOTE:
I will only cover the implementation details, for the mathematical details
please read [10].
Implementation Constraints
The objective is to compute 5000 π digits, time it, and
then compare timings with my previous results (see
Example: π Shootout above).
IANS, π ~ 2*Vk,n. If k = 0
then only Viète's original formula (Eq. 3) is computed to n terms.
If k > 0 then we get the benefit of Kreminski's discovery (Eq. 2).
Note that Vk,n contains no costly square root and that small
values for k can have a tremendous impact on the acceleration of Viète's
Formula.
Table 2: Values for k
and n for computing at least 5000 digits of π
|
| k |
n |
Vk,n digits |
V0,n digits |
| 0 |
8334 |
5001 |
5001 |
| 1 |
4166 |
5002 |
2508 |
| 2 |
2776 |
5002 |
1672 |
| 3 |
2081 |
5002 |
1253 |
| 4 |
1663 |
5002 |
1002 |
| 5 |
1385 |
5004 |
834 |
| 10 |
750 |
5004 |
452 |
| 50 |
134 |
5003 |
81 |
| 100 |
27 |
5004 |
16 |
Observe from Table 2 how small values of k significantly
reduce n and that a small n with k = 0 (V0,n) produces only a
handful of accurate digits. You may also have observed that V0,n digits
~ 0.6 * n. Small n big k, right? Well, to know
exactly what the optimal values are, we need to know the iterative count for Vk,n and V0,n and
the cost (in time) of each iteration.
Vk,n will iterate 2k-1 times! You are better off computing with only Viète's
Formula. However, if you cache computed values of Vk,n,
then only k(k+1)/2 iterations are required. IOW, your
scaling changes from O(2k) to O(k2),
and that's a world of difference. The size of the cache will need to be
k(k+1)/2 and will be hit k(k+1)-2k+1 times.
As Vk,n iterates certain values of V0,n will be
required with the maximum number of terms set to k+n+1. To
save time and avoid recomputing
V0,n,
V0,n will be computed once up to k+n+1, with
the last k+1 values cached. This cache will be used 2k+1
times.
It should be apparent that k controls the size of
our caches and therefore the amount of RAM used, whereas n only impacts
time (square root, square root, etc...). Since k scales quadratically and n scales linearly
there will be a point where the cost to compute with a large k, small
n (bounded by a maximum number of digits desired) exceeds a smaller k
with a larger n.
We have a big (or should I say small
:-) problem--RAM. For 5000 digits there is an optimum k and n
for the 50g, but we run out of memory around k = 13. Each number
consumes 2516 bytes of memory. We need to cache k(k+1)/2 + k+1
numbers, plus Vk,n has a maximum recursion depth of k+1.
So that's k(k+1)/2 + k+1 + k+1 or ((k+2)(k+3)/2)
* 2516 bytes = 301,920 bytes of memory when k = 13. My 50g only has ~ 322K free
when my program starts.
The plot below illustrates the relationship between k
and memory.
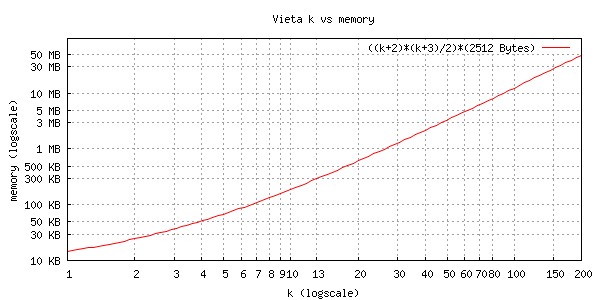
Results
Trial 1
Below is a plot and a table of k vs. time for my first Kreminski's Viète
program (vieta.c). NOTE:
n was computed
based on the maximum number of digits π (5000) desired.
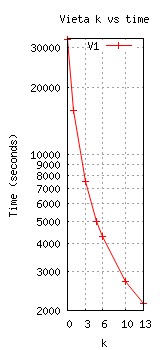 |
| k |
n |
T(V0,n+k+1) |
T(Vk,n) |
| 0 |
8334 |
32634 |
0 |
| 1 |
4166 |
15785 |
0 |
| 3 |
2081 |
7597 |
0 |
| 5 |
1385 |
4992 |
0 |
| 6 |
1186 |
4270 |
0 |
| 10 |
750 |
2709 |
0 |
| 13 |
586 |
2141 |
1 |
|
Clearly as k increases, n decreases reducing
the number of costly square root operations. The acceleration works and works well. Almost no time
is spent on the Vk,n recursion and the time spent on square
root operations is significantly reduced. Unfortunately caching Vk,n and V0,n
consumes too much RAM limiting k < 14.
Trial 2
My second Kreminski's Viète
program (vieta2.c) is identical to my
first except instead of using RAM to cache Vk,n, I used a file
on my SD card. This is an ideal situation since relatively very little
time is spent in the the Vk,n recursion and the type of access is
relatively large sequential reads and writes (2516 bytes). A plot of
vieta.c and
vieta2.c results:
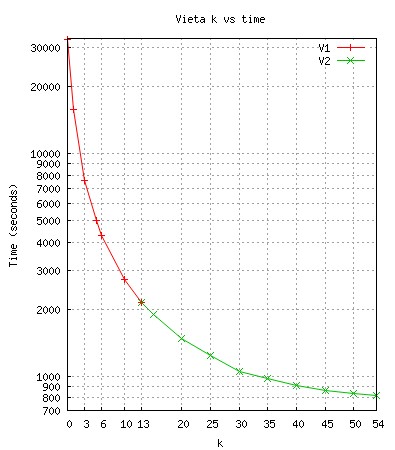
Kreminski's Viète continues to provide
acceleration. With the Vk,n cache offloaded to SD, more
RAM can be used to cache V0,n and the overhead of the Vk,n
recursion. Below is a table of the time spent computing V0,n and Vk,n:
| k |
n |
T(V0,n+k+1) |
T(Vk,n) |
T(V0,n+k+1)+T(Vk,n) |
|
13 |
586 |
2141 |
5 |
2146 |
|
15 |
511 |
1885 |
6 |
1891 |
|
20 |
384 |
1464 |
11 |
1475 |
|
25 |
305 |
1215 |
18 |
1233 |
|
30 |
250 |
1050 |
26 |
1076 |
|
35 |
210 |
938 |
36 |
974 |
|
40 |
179 |
857 |
47 |
904 |
|
45 |
155 |
801 |
61 |
862 |
|
50 |
134 |
757 |
75 |
832 |
|
54 |
120 |
731 |
89 |
820 |
At k = 54 vieta2 ran out of RAM. 298872 bytes were
used just to cache V0,n and the overhead of the Vk,n
recursion. The good new is that over 3.7 MBs of the SD card were utilized to cache Vk,n.
The SD card as a RAM replacement in this case worked out very well.
However, there was a small performance hit. If you compare the k =
13 timings of the first two trials you will notice a 4 second performance drop.
Given the ability to increase k beyond 13, caching Vk,n
to SD is a superior solution.
The next
candidate for offload will be V0,n.
Trial 3
My third Kreminski's Viète
program (vieta3.c) is identical to my
second except instead of using RAM to cache V0,n, I
again used a file
on my SD card. This again is an ideal situation since relatively very little
time is spent reading and writing V0,n. A plot of
vieta.c,
vieta2.c, and
vieta3.c results:
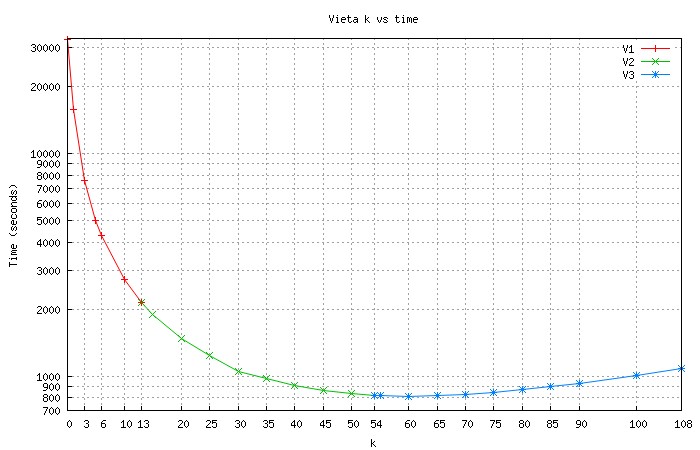
No surprise that at k = 108 (2*54) I ran out of memory.
Since the V0,n cache was moved to SD the Vk,n
recursion overhead can now be doubled. Below is a table of the time spent
computing V0,n and Vk,n:
| k |
k(k+1)/2 |
n |
T(V0,n+k+1) |
T(Vk,n) |
T(V0,n+k+1)+T(Vk,n) |
|
54 |
1485 |
120 |
732 |
88 |
820 |
|
55 |
1540 |
117 |
727 |
92 |
819 |
|
60 |
1830 |
102 |
702 |
111 |
813 |
|
65 |
2145 |
89 |
685 |
132 |
817 |
|
70 |
2485 |
78 |
676 |
154 |
830 |
|
75 |
2850 |
67 |
666 |
179 |
845 |
|
80 |
3250 |
58 |
662 |
206 |
868 |
|
85 |
3655 |
49 |
659 |
235 |
894 |
|
90 |
4095 |
41 |
660 |
266 |
926 |
|
100 |
5050 |
27 |
667 |
336 |
1003 |
|
108 |
5866 |
17 |
677 |
399 |
1076 |
So the ideal k for the 50g is around 60 when
computing at least 5000 digits of π. With k > 60, Vk,n
has too many iterations and its time increase is greater than the time saved by
a smaller n.
Finding the
optimal k and n
NOTE: The left and right brackets [] represent
the floor function.
Finding n from k is also given to us by
Kreminski [10]. The number of accurate π digits for any k and n > .6(k+1)n
- [(log10(Ck)], where
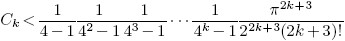
E.g. if k = 60 and n = 102, then .6(k+1)n
- [(log10(Ck)] = .6*6222 - [(log10(2.6*10-1283)]
= 3733 + 1283 = 5016. If n were one less then the number of digits
would be 4979. Simple algebra can be used to find n given k
and the maximum number of digits to compute.
Finding the optimal k and n requires a bit of work.
If you know the time for each Vk,n and V0,n
iteration you could (with some work) obtain a method to deliver reasonable k
and n constants for a fixed number of digits desired in minimum time.
A challenge with this is that the time for each iteration is not constant.
E.g. vieta3.c, n = 120, V0,n+k+1
iteration time = 732/175 = 4.81 seconds/iteration, and n = 17, V0,n+k+1
iteration time = 677/126 = 5.37 seconds/iteration.
However it is still possible to get a starting point.
The following chart was created using the k = 80 data above:
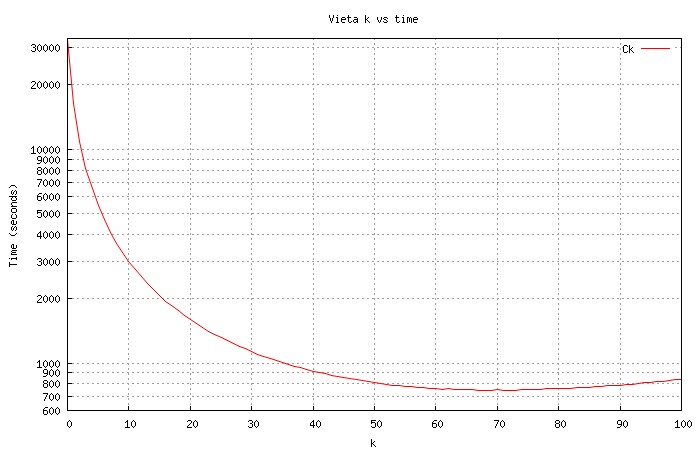
If you think the chart above looks similar to the previous chart, it does.
This chart suggests looking around 70 for the optimal value for k.
Although we already know (via brute force) that k = 60 is faster, its not
a bad estimate based on the results on a single run. And the difference in
time from k = 60 to k = 70 is only 17 seconds (~2.1% increase).
Viète vs. The World
How did Kreminski's Viète stack up against my previous
results?
| Place |
Algorithm
|
AP/MP Library
|
Digits
|
Time(s)
|
Bytes(RAM) |
Bytes(SD) |
| 1 |
Chudnovsky |
FFT |
8109 |
36 |
277,168 |
0 |
| 2 |
Størmer
Arctangent |
Internal |
5001 |
38 |
11,208 |
0 |
| 3 |
Machin Arctangent |
Internal |
5001 |
44 |
15,368 |
0 |
| 4 |
Spigot |
Internal |
5000 |
46 |
77,092 |
0 |
| 5 |
Gauss AGM (Schönhage Variant) |
decNumber |
5005 |
122 |
31,104 |
0 |
| 6 |
Chudnovsky |
decNumber |
5006 |
375 |
Unknown |
0 |
| 7 |
Viète-Kreminski |
decNumber |
5004 |
813 |
153,476 |
4,757,756 |
| 8 |
Viète |
decNumber |
5001 |
32634 |
5,032 |
0 |
Viète Accelerated while more interesting (IMHO) only bests Viète
without the aid of acceleration. However, recreationally speaking, Viète
and Spigot are tied at number one on my list.
The Code
All of the source and object code for this example can be
obtained from
http://sense.net/~egan/hpgcc/vieta_accelerated.tgz.
To install open an Xterm and type:
cd ~/hpgcc
wget
http://sense.net/~egan/hpgcc/vieta_accelerated.tgz
tar zxvf vieta_accelerated.tgz
NOTE: You must upgrade the
libfsystem support if using 2GB SD
cards, see HPGCC 2GB SD Card Support
for more details.
Wrapper
The wrapper is similar to others used in this document with
the exception of the last two statements:
OBJ-> EVAL. If there is no error
the wrapper expects some UserRPL code on the stack in text form that needs to be
converted to a program object then evaluated. More on this later.
%%HP: T(3)A(R)F(.);
\<< \-> k n
\<<
n \->NUM
k \->NUM
"EXTEND/VIETA3" 3 \->TAG EVAL
IF
THEN
DOERR
END
OBJ\-> EVAL
\>>
\>>
Usage
All three versions take two arguments: k and
n, and will calculate no more than 5000 π digits. If k = 0, then classic Viète will be used. If n
= 0, then n is calculated using Ck (max digits = 5000). If k =
n = 0, then k is calculated based on the amount of free memory and
n is calculated based on Ck (max digits = 5000).
Example screen output:
Press ON/CANCEL to exit.
Example stack output:

Code with Comments
NOTE: I will only comment on code that introduces HPGCC
capabilities not covered in other sections of this document.
libfsystem
for Arrays
libfsystem is a high-speed, feature
rich, SD card I/O library created by the HPGCC team.
NOTE: libfsystem
is not available as part of HPAPINE. Search for HPAPINE in the source if
you want an example of how to use stdio.
This option (stdio) is available for
HPGCC as well, but does not perform as well as
libfsystem and is unstable (issues with seeking).
NOTE: If you have a 2GB SD card installed
please verify that libfsystem has been
updated, see HPGCC 2GB SD Card Support
for details.
Leveraging
libfsystem as a RAM replacement for
large arrays is fairly straightforward:
-
You will need the following lines at the beginning
of your program:
#include <fsystem.h>
extern U32 syscallArg0(U32 index);
The syscallArg0
statement is used to release the SD card back to the UserRPL 50g shell
environment. If this call is not made before returning to UserRPL the SD
card will be unavailable until the 50g is power cycled.
-
Replace array pointers with
libfsystem pointers and define
filenames, e.g.:
decNumber *V, *V0;
becomes:
FS_FILE *vfp, *v0fp;
char *vcache = "vcache.dat", *v0cache = "v0cache.dat";
- Replace array allocations and initializations, e.g.:
if((V = malloc((k*(k+1)/2)*sizeof(decNumber))) == NULL && k > 0) {
char errormsg[50];
sprintf(errormsg,"Failed to allocate %d bytes of memory for V",(int) ((k*(k+1)/2)*sizeof(decNumber)));
sat_stack_push_string(errormsg);
sat_push_real(1);
return(0);
}
for(i = 0; i < k*(k+1)/2; i++)
decNumberZero(&V[i]);
becomes:
FSOpen(vcache, FSMODE_WRITE | FSMODE_READ | FSMODE_MODIFY, &vfp);
if (vfp == NULL) {
char errormsg[50];
sprintf(errormsg,"Cannot open: %s",vcache);
sat_stack_push_string(errormsg);
sat_push_real(1);
return(0);
}
else {
decNumber zero;
decNumberZero(&zero);
for(i = 0; i < k*(k+1)/2; i++)
FSWrite((char*)&zero,recordsize,vfp);
}
-
Replace array reads, e.g.:
decNumberCopy(p,&V[addr]);
becomes:
FSSeek(vfp,(addr*recordsize),0);
FSRead((char*)&V,recordsize,vfp);
- Replace array writes, e.g.:
decNumberCopy(&V[addr],p);
becomes:
FSSeek(vfp,(addr*recordsize),0);
FSWrite((char*)p,recordsize,vfp);
-
Finally, close and remove files, and then reset the SD
card:
FSCloseAndDelete(vfp);
FSCloseAndDelete(v0fp);
syscallArg0(19);
For more detail closely compare
vieta.c with
vieta3.c.
NOTE: You cannot easily mix
libfsystem and
stdlib file calls (f*).
If this is required (and is, in this example), then you must reset the SD card
first before using fgetc,
fprintf, etc...
Arbitrary Text Cursor Positioning
When you execute any of the programs in this example you will notice
a number of dynamic screen updates, e.g.:

This is achieved with the
gotoxy(x,y) function, where
x and
y are the number of columns and
rows (base 0) to move to. E.g.:
gotoxy(18,5);
printf("100%%");
will print the text 100%
starting at column 19 row 6 if the upper left corner is considered 1,1.
Computer Generated UserRPL Code
At the end of each vieta*.c
program 4 values with matching tags are pushed to the stack:
sat_push_zint_llong(k);
sat_stack_push_string("k");
sat_push_zint_llong(n);
sat_stack_push_string("n");
sat_push_zint_llong(num);
sat_stack_push_string("digits");
sat_push_zint_llong(end - start);
sat_stack_push_string("time");
In previous examples a custom wrapper was created to pair
tag to value. This wrapper was hard coded to a specific number of pairs
requiring an update if the C program changed. To avoid this it is possible
to generate a UserRPL program, push it to the stack, and have it executed by a much simpler
wrapper, leaving only the C program to control what gets pushed to the stack and
how it is processed.
First, define any special characters. You can obtain
the decimal representation of any special character using the CHARS menu on the
50g (Right-shift EVAL), e.g.:
#define PROG_LEFT 171
#define PROG_RIGHT 187
#define ARROW_RIGHT 141Next, write your program to a buffer and push to
the stack: sprintf(buf,"%c 7 4 FOR i %cTAG i ROLLD -1 STEP %c",PROG_LEFT,ARROW_RIGHT,PROG_RIGHT);
sat_stack_push_string(buf);
Finally, define your wrapper:
%%HP: T(3)A(R)F(.);
\<< \-> k n
\<<
n \->NUM
k \->NUM
"EXTEND/VIETA3" 3 \->TAG EVAL
IF
THEN
DOERR
END
OBJ\-> EVAL
\>>
\>>
This wrapper is similar to many in this document, except
that a program is expected to be pushed to the stack and executed with
EVAL if no error occurred.
| Sidebar: Memory Card Performance
In the ~/hpgcc/sdbench directory is a simple sequential SD card
benchmark program. This program will test various block sizes for read
and write performance and then create an sdbench.xls
file on the SD card suitable for use with MS Excel.
Usage
sdbench takes a
single argument: file size in megabytes. The block size range
is hard coded as #define statements.
The default uses a range of block sizes from 28 to 212
bytes inclusive. When the last block size is tested the program will halt
and wait for CANCEL to be pressed.
Creating 3D Bar Plots in Excel
sdbench.xls is not a properly formatted Excel file.
However, if you tab delimit your fields and give the file a
.xls extension, then Excel will read
the file as if it were an Excel file--no questions asked. Just pop your SD
card into your SD card reader and double-click on the file and presto Excel will
open window something like this:
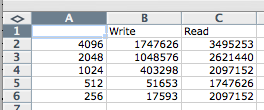
To create a 3D plot simply highlight all the numbers with
the headers (e.g. A1 through C6) and use the Chart Wizard or equivalent to
select the chart type that looks similar to the three charts to the right.
NOTE: To make the charts more readable I
divided the Write and Read columns by 1024 to report KB/s.
Shootout
I rounded up every SD card I could find:
| Brand/Model
|
Capacity
|
Chart Name
|
| ativa 60x |
2GB |
ativa60x |
| Kingston |
128MB |
king128 |
| Lexar |
128MB |
lex128 |
| Lexar |
64MB |
lex64 |
| SanDisk |
1GB |
sd1gb |
| SanDisk microSD
|
2 GB |
micro2gb |
| SanDisk ultra II |
1 GB |
ultra1gb |
For each card I used a 10MB file. Below is a
comparison of just the 4KB block size results.
Summary
Clearly different SD cards perform at different rates.
Read performance was incredibly fast for all cards (at least 2MB/second!), this
performance comes from libfsystem.
What is the impact of different SD cards on
vieta*.c? That is a question
left for the reader.
|
Final Words
The treatment of
libfsystem in this example is not very rigorous or safe. In the
interest of performance I omitted any error checking. Before leveraging
libfsystem in your code, please read the
libfsystem documentation.
UPDATE:
Iterative vs. Recursive
Less than 24 hours after I published this example I
received an interesting message from Hugh Steers:
|
I claim you only need k+1 numbers to calculate Vk,n.
What you do, is fill out a k+1 array with V0,n .. V0,n+k and reduce this
"row" k times with the recurrence relation until finally the first slot of the
array is the value of Vk,n.
|
Brilliant! Clearly this is going to significantly
reduce memory usage. The
memory usage for vieta.c is ((k+2)(k+3)/2)
* 2516 bytes whereas the memory usage for Hugh's iterative approach is (k+1)
* 2516 bytes. E.g. for k = 60 that would be ~9.37 MB (recursive)
vs. less than 150 KB (iterative).
Hugh was also kind enough to provide a C++ double precision
snippet to illustrate his point. IANS, all that is different between the
recursive and iterative versions is the Vieta
function (Vk,n). For complete details compare vieta.c
and vieta4.c.
A plot of
vieta2.c,
vieta3.c, and
vieta4.c results:
The iterative count for the recursive and iterative Vk,n
remains k*(k+1)/2 and the computation required for each iteration
is approximately the same, so why does the iterative Vk,n run
faster as k gets larger? Simple really, using the SD card as a RAM
replacement will always be slower than RAM. Without the SD both perform
the same. However, with such a small k (13) it is hard to tell.
If skeptical try it yourself on your PC/Mac using 10,000 or 20,000 digits.
Both programs perform the same, but memory usage is measurably different.
So what is Hugh's suggestion for using SD as a RAM
replacement? Don't! Hugh computed the same problem with the same
algorithm smarter whereas I computed it harder.
How did Hugh's Kreminski's Viète stack up against my previous
results?
| Place |
Algorithm
|
AP/MP Library
|
Digits
|
Time(s)
|
Bytes(RAM) |
Bytes(SD) |
| 1 |
Chudnovsky |
FFT |
8109 |
36 |
277,168 |
0 |
| 2 |
Størmer
Arctangent |
Internal |
5001 |
38 |
11,208 |
0 |
| 3 |
Machin Arctangent |
Internal |
5001 |
44 |
15,368 |
0 |
| 4 |
Spigot |
Internal |
5000 |
46 |
77,092 |
0 |
| 5 |
Gauss AGM (Schönhage Variant) |
decNumber |
5005 |
122 |
31,104 |
0 |
| 6 |
Chudnovsky |
decNumber |
5006 |
375 |
Unknown |
0 |
| 7 |
Viète-Kreminski (Steers) |
decNumber |
5004 |
740 |
166,056 |
0 |
| 8 |
Viète-Kreminski |
decNumber |
5004 |
813 |
153,476 |
4,757,756 |
| 9 |
Viète |
decNumber |
5001 |
32634 |
5,032 |
0 |
Thanks again Hugh.
NOTE:
http://sense.net/~egan/hpgcc/vieta_accelerated.tgz has
been updated to include vieta4.c.
Summary
The greatest advantage with C is portability. Most of
the C code in this document was written by others and ported to the 50g with
little to no effort. This increases the potential code base beyond all
UserRPL, SysRPL, and Saturn assembly code combined.
Google is a great place to shop for numerical C code and
libraries. Another great source is the book Numerical Recipes in C,
2nd Ed. This text is freely available from
http://nr.com. Because of copyright issues I was unable to use and
publicly post any code from this text.
With HPGCC the 50g application possibilities are nearly
infinite. Speed, portability, and ease of use are all factors that make
50g C development very practical.
Thanks
I would like to thank the following:
The HPGCC Team: Ingo Blank, Claudio Lapilli, Benjamin
Maurin. HPGCC was the most critical component of this document.
Jean-Yves Avenard:
OS/X HPGCC port.
Khanh-Dang NGUYEN THU-LAM, the author of HPAPINE.
Without HPAPINE I would have lost interest because of the time it takes to test
on the 50g.
Philippe Salmon, the author of HPStack, HPParser, and
HpgBmp.
S. L. Moshier, the author of c9x-complex.
Timothy A. Davis, the author of CSparse.
Jörg Arndt and Christoph
Haenel, the authors of π Unleashed and the modified spigot algorithm.
Jeremy Gibbons, the author of the unbounded spigot
algorithm.
Tom St. Denis, the author of LibTomMath.
J.W. Stumpel, the original author of Machin.
Stefan Spännare and Takuya Ooura, authors of Chudnovsky/FFT.
Srpcic Silvo, the author of Pi50g, and for helping with the Saturn/Assembly
vs. ARM/C
π shootout.
Ken Clarkson, author of
2dch.c.
Steven Fortune, author of
Voronoi.
The Free Software Foundation for creating first class open
source development tools.
The Cygwin/X team for making FSF projects available for
Windows.
Rick Kreminski, Viète Acceleration.
Hugh Steers, Iterative Viète Acceleration.
And, all that took the time to send feedback and
suggestions.
Thanks!
References
[1] http://gcc.gnu.org/
[2] http://www.hydrix.com/Download/Hp/hpgcc/
[3] http://phsalmon.club.fr/phsalmon/hpstack/hpstack.html
[4] http://pagesperso-orange.fr/kdntl/hp49/hpapine/
[5] http://mathworld.wolfram.com/LogGamma.html
[6] http://www.cise.ufl.edu/research/sparse/CSparse/
[7] http://crd.lbl.gov/~dhbailey/dhbpapers/dhb-kanada.pdf
[8] http://libtom.org/?page=features&newsitems=5&whatfile=ltm
[9]
http://documents.wolfram.com/mathematica/Demos/Notebooks/CalculatingPi.html
[10] R. Kreminski, Pi to Thousands of Digits from Vieta's
Formula, Mathematics Magazine, Vol. 81, No. 3, June 2008, 201-207
Change Log
Version 1.00: Initial release. Jan/2008.
Version 1.01: Improved Cygwin installation notes. Minor spelling
corrections. Added Change Log. May/2008.
Version 1.02:
hpgccenv updated in hpgcc.tgz to
address issues with latest Cygwin. May 11 2008.
Version 1.03: "NOTE: XP users must have
SP2 or later installed to build HPAPINE binaries." added to
HPAPINE 101.
May 12 2008.
Version 1.04: Added Linux support to notes and a Linux tarball. May
29 2008.
Version 1.05: Added notes on how to read the locally
stored HPGCC documentation in the Support section.
June 1 2008.
Version 1.10: Nov 30 2008.
Version 1.11: Error in Viète
Accelerated. In the section
libfsystem for Arrays,
fopen should be
FSOpen. Dec 1
2008.
Version 1.12: Added
UPDATE: Iterative vs.
Recursive to Viète Accelerated. Dec 9
2008.
Hits since: Sat April 1 00:00:00 UTC 2008: